本章概述

本章对一般线性方程组的求解进行讨论。首先介绍了用消元法解线性方程组。重点介绍了向量的线性表示，线性相关，线性无关的概念及其相关性质。最后介绍了齐次线性方程组解的结构，非齐次齐次线性方程组解的结构。

学习目标

1.本章重点是齐次线性方程组解的结构与非齐次线性方程组解的结构，难点是n维向量的线性相关与线性无关的概念。

2.掌握用初等变换解线性方程组。

3.掌握向量的线性相关与线性无关的概念，并能讨论一些简单问题。

4.掌握矩阵的秩的概念，并会求矩阵的秩。

5.掌握线性方程组有解判别法。

6. 掌握齐次线性方程组解的结构与非齐次线性方程组解的结构，并能求出线性方程组的全部解。

知识结构框图

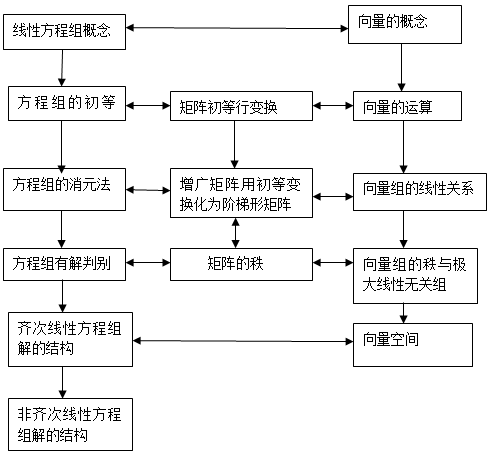
重点难点解析与学习建议

本章是围绕线性方程组理论的三个中心问题展开讨论的。

首先介绍了古老而广泛使用的求解线性方程组的消元法，主要通过线性方程组的初等变换求同解的线性方程组，即对方程组的对应的增广矩阵用初等变换化为阶梯形矩阵求解。其次是对线性方程组的解的情况讨论，引入了向量的线性相关性，秩与极大线性无关组，矩阵秩的概念，给出了线性方程组有解的充分必要条件。最后利用向量空间概念研究了线性方程组的解的结构。

向量组的线性相关性是线性代数中的一个重点也是一个难点，对逻辑推理有较高的要求，相对比较抽象。在学习本部分内容时，无论是判断，证明或计算，关键在于要深刻理解基本概念，搞清其相互之间的关联，要学会用定义来推导论证，注意推导过程中逻辑的正确性。

含有参数的线性方程组求解要熟练掌握，因为它综合考查矩阵的秩的确定，线性方程组解的情况的判定，求解方法及解的结构。

课前提问

1、你能给出线性方程组解的定义吗？

2、你能给出线性方程组同解的定义，并举例说明吗？

3、你能用矩阵的初等变换说明线性方程组求解的消元方法吗？并举例说明吗？

4、你能给出向量组的线性相关与线性无关的定义吗，并举个例子说明？

5、给出矩阵的秩的定义，并举个例子说明计算方法？

6、叙述线性方程组有解判别法。

7、齐次线性方程组解有哪两条性质？你能叙述出来吗？

8、你能给出齐次线性方程组基础解系的定义吗？

9、叙述齐次线性方程组解的结构定理。

10、叙述非齐次线性方程组解的结构定理。

11、你能用矩阵初等变换法求齐次线性方程组的基础解系吗？请举个例子。

12、你能用矩阵初等变换法求非齐次线性方程组的全部解集合吗？请举个例子。

14、你认为这一章中的哪些实例或者练习题最有意思？哪些题目感觉较难，作为笔记的内容之一，试着总结一下.