当前位置:课程学习>>第四章 线性方程组>>拓展资源>>拓展学习
学习指导
一、内容提要
1.基本概念
1)向量组的线性表示、向量组的线性相关、向量组的线性无关,向量组的线性等价,向量组的极大无关向量组,向量组的秩。
2)矩阵的秩,方程组的系数矩阵与增广矩阵,方程组同解,齐次线性方程组,非齐次线性方程组,齐次线性方程组的基础解系,非齐次线性方程组特解,线性方程组的一般解与通解.
2.基本结论
1)任意![]() 个
个![]() 维向量组一定线性相关;行列式的基本性质;
维向量组一定线性相关;行列式的基本性质;
2)两个线性无关的等价向量组,必含有相同个数的向量;
3)等价的向量组有相同的秩;
4)线性方程组有解的充分必要条件是系数矩阵的秩与增广矩阵的秩相等;
5)齐次线性方程组有非零解充分必要条件是系数矩阵的秩小于未知量个数,此时有基础解系;
6)非齐次线性方程组在有解时,其全部解为它的一个特解与导出组的基础解系的线性组合。
3.基本方法
1)矩阵的初等变换法求向量组的极大线性无关组;
2)矩阵的初等行变换解线性方程组;
4.需要说明的问题
本章是围绕线性方程组理论的三个中心问题展开讨论的。
首先介绍了古老而广泛使用的求解线性方程组的消元法,主要通过线性方程组的初等变换求同解的线性方程组。其次是对线性方程组的解的情况讨论,引入了向量的线性相关性,秩与极大线性无关组,矩阵秩的概念,给出了线性方程组有解的充分必要条件。最后利用向量空间概念研究了线性方程组的解的结构。
向量组的线性相关性是线性代数中的一个重点也是一个难点。在学习本部分内容时,无论是判断,证明或计算,关键在于要深刻理解基本概念,搞清其相互之间的关联,要学会用定义来推导论证,注意推导过程中逻辑的正确性。
齐次线性方程组与非齐次线性方程组的求解是线性方程组中重要而简单问题,同学们必须熟练掌握。
含有参数的线性方程组求解要熟练掌握,因为它综合考查矩阵的秩的确定,线性方程组解的情况的判定,求解方法及解的结构。
二、精选例题解析
例1设![]() 问
问
(1)![]() 为何值时,
为何值时,![]() 线性无关?
线性无关?
(2)![]() 为何值时,
为何值时,![]() 线性相关?并把
线性相关?并把![]() 表为
表为![]() 的线性组合。
的线性组合。
解 ![]() 对应的行列式
对应的行列式
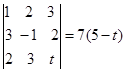
(1)当 ![]() ,即
,即![]() 时,则
时,则![]() 线性无关。
线性无关。
(2)当 ![]() ,即当
,即当 ![]() ,则
,则![]() 线性相关。
线性相关。
令![]() ,,则有线性方程组
,,则有线性方程组
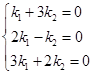
解得![]() ,所以
,所以![]() 。
。
例2 判别下例论断哪些是对的,哪些是错的。对的,加以证明,错误的,举反例说明
(1)若![]() 线性相关,则其中每一个向量都是其余向量的线性组合;
线性相关,则其中每一个向量都是其余向量的线性组合;
(2)如果有一组不全为零的数![]() ,使,
,使,
![]()
则![]() 线性无关;
线性无关;
(3)若存在一组全为零的数,使![]()
则![]() 线性无关;
线性无关;
(4)若两个![]() 维向量组
维向量组![]() 与
与![]() 均线性无关,则向量组
均线性无关,则向量组![]() 线性无关;
线性无关;
(5)若两个![]() 维向量组
维向量组![]() 与
与![]() 均线性无关,则向量组
均线性无关,则向量组![]() 线性无关;
线性无关;
(6)![]() 线性无关的充分必要条件是任意两个向量线性无关。
线性无关的充分必要条件是任意两个向量线性无关。
解 (1)错。事实上向量组![]() 是线性相关,但
是线性相关,但![]() 不能由
不能由![]() 线性表示。
线性表示。
(2)错。因为只有对任何一组不全为零的数![]() ,
,![]() 才能说明
才能说明![]() 线性无关。只有一组数时,不能说明。例如
线性无关。只有一组数时,不能说明。例如![]() 存在着
存在着![]() 使得
使得![]() ,但
,但![]() 显然线性相关。
显然线性相关。
(1) 错。一组全为零的数![]() ,对任何
,对任何![]() 个向量的向量组
个向量的向量组![]() ,均有
,均有![]() 成立。例如
成立。例如![]() ,
,![]() 线性相关,但
线性相关,但![]() 。
。
(2)错。例![]() 线性无关,
线性无关,![]() 线性无关,而
线性无关,而![]() 是3个2维向量,线性相关。
是3个2维向量,线性相关。
(3)错。例![]() 线性无关,
线性无关,![]() 线性无关。而
线性无关。而![]() 线性相关。
线性相关。
(4)命题中必要性成立,充分性不成立。例如![]() 它们两两线性无关,但
它们两两线性无关,但![]() 线性相关。
线性相关。
必要性证明 用反证法,假设任何两个向量![]() 线性相关,则有不全为零的数
线性相关,则有不全为零的数![]() ,使
,使![]() ,于是存在不全为零的数
,于是存在不全为零的数![]() ,使
,使![]() ,所以,
,所以,![]() 线性相关,矛盾。
线性相关,矛盾。
例3 求![]() 内向量组的极大线性无关组
内向量组的极大线性无关组
![]() ,
,
![]() 。
。
解 把它们作为列向量组成![]() 矩阵
矩阵![]() ,再对
,再对![]() 作初等行变换化为阶梯形矩阵
作初等行变换化为阶梯形矩阵
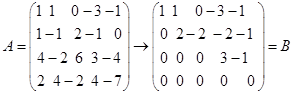
![]() 所以
所以![]() 的列向量组的一个极大无关组为第1,2,4列向量,因此,
的列向量组的一个极大无关组为第1,2,4列向量,因此,![]() 的列向量组
的列向量组![]() 的一个极大无关组为
的一个极大无关组为![]() 。
。
例4 设![]() ,
,![]() ,
,![]() 线性无关,证明
线性无关,证明![]() ,
,![]() ,
,![]() 也线性无关.
也线性无关.
证明 设![]()
整理得 ![]()
因为![]() 线性无关,所以有
线性无关,所以有
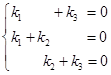
解得只有唯一零解![]() ,所以
,所以![]() ,
,![]() ,
,![]() 也线性无关.
也线性无关.
例5 设![]() ,
,![]() ,
,![]() ,
,![]() 是一组
是一组![]() 维向量,已知单位向量
维向量,已知单位向量![]() ,
,![]() ,
,![]() ,
,![]() 可被它们线性表出,证明:
可被它们线性表出,证明:![]() ,
,![]() ,
,![]() ,
,![]() 线性无关.
线性无关.
证明 ![]() 的秩为
的秩为![]() ,则
,则![]() 。而
。而![]() 的秩为
的秩为![]() ,由假设向量
,由假设向量![]() ,
,![]() ,
,![]() ,
,![]() 可被
可被![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,由上题结论有
线性表出,由上题结论有![]() ,所以
,所以![]() ,因此,
,因此,![]() ,
,![]() ,
,![]() ,
,![]() 线性无关。
线性无关。
例6 设![]() ,
,![]() ,
,![]() ,
,![]() 是一组
是一组![]() 维向量,证明:
维向量,证明:![]() ,
,![]() ,
,![]() ,
,![]() 是线性无关的充分必要条件是任一
是线性无关的充分必要条件是任一![]() 维向量都可以被它线性表出
维向量都可以被它线性表出
证明 充分性 设任意![]() 维向量均可由
维向量均可由![]() ,
,![]() ,
,![]() 线性表示,则单位
线性表示,则单位![]() ,
,![]() ,
,![]() ,
,![]() 可由
可由![]() ,
,![]() ,
,![]() ,
,![]() 线性表出,由上题知
线性表出,由上题知![]() ,
,![]() ,
,![]() ,
,![]() 线性无关。
线性无关。
必要性 设![]() ,
,![]() ,
,![]() ,
,![]() 线性无关,则
线性无关,则![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的极大无关组,因此,任意
的极大无关组,因此,任意![]() 维向量均可由
维向量均可由![]() ,
,![]() ,
,![]() 线性表示。
线性表示。
例7 已知![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 有相同的秩,证明:
有相同的秩,证明:![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 等价.
等价.
证明 由于![]() ,
,![]() ,
,![]() ,
,![]() 可由
可由![]() ,
,![]() ,
,![]() ,
,![]() 线性表示,只需证
线性表示,只需证 ![]() ,
,![]() ,
,![]() ,
,![]() 可由
可由![]() ,
,![]() ,
,![]() ,
,![]() 线性表示,即
线性表示,即![]() 可由
可由![]() ,
,![]() ,
,![]() ,
,![]() 线性表示。
线性表示。
设![]() ,
,![]() ,
,![]() ,
,![]() 的极大线性无关组为
的极大线性无关组为![]() ,由于向量组
,由于向量组![]() ,
,![]() ,
,![]() ,
,![]() 与
与 ![]() ,
,![]() ,
,![]() ,
,![]() 的秩相等,从而
的秩相等,从而![]() 也是
也是![]() ,
,![]() ,
,![]() ,
,![]() 极大线性无关组,故
极大线性无关组,故![]() 可由
可由![]() 线性表示,从而可由
线性表示,从而可由![]() ,
,![]() ,
,![]() ,
,![]() 。
。
例8.若向量组![]() 线性相关,向量组
线性相关,向量组![]() 线性无关,证明:(1)
线性无关,证明:(1)![]() 可由
可由![]() 线性表示;
线性表示;
(2) ![]() 的表示式是唯一的。
的表示式是唯一的。
证明 (1) 向量组![]() 线性相关,则存在不全为零的数
线性相关,则存在不全为零的数![]() ,使
,使![]() ,下证
,下证![]() 即可。反证,若
即可。反证,若![]() 则
则![]() ,所以,
,所以,![]() 性相关,矛盾,所以
性相关,矛盾,所以![]() ,于是有
,于是有![]() 。
。
(2) 设![]() ,
,![]()
则有两式相减,![]()
因为向量组![]() 线性无关,所以
线性无关,所以
![]() ,
,
因此![]() 。唯一性得证。
。唯一性得证。
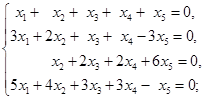
解 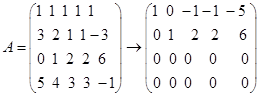
同解方程组为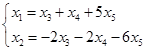 ,
,
令![]() ,则得
,则得![]() ,故
,故![]() ;令
;令![]() 则得
则得![]() ,故
,故![]() ;令
;令![]() ,则
,则![]() ,故
,故![]() ,所以
,所以
基础解系为![]() ,
,![]() ,
,![]() 。
。
全部解为![]()
![]() 是任意的。
是任意的。
例10 问![]() 取何值时,方程组
取何值时,方程组
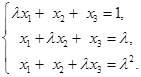
有唯一解;无解;有无穷多解。并在有解时,求出全部解。
解 (1)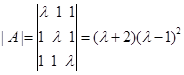
当![]() ,方程组有唯一解。利用克拉默法则,得
,方程组有唯一解。利用克拉默法则,得![]()
当![]() ,
,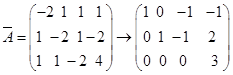 ,
,![]() ,方程组无解。
,方程组无解。
当![]() ,
,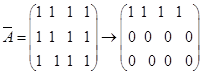 ,
,![]() ,方程组有无穷多解。同解方程组
,方程组有无穷多解。同解方程组![]() ,通解
,通解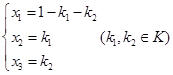
例11 若向量![]() 是齐次线性方程组
是齐次线性方程组![]() 的一个基础解系。向量
的一个基础解系。向量![]() 满足
满足![]() ,求证:向量组
,求证:向量组![]() 线性无关。
线性无关。
证明:设有![]() 使得
使得
![]()
则 ![]()
于是 ![]()
所以 ![]()
因为![]() ,所以
,所以![]() ,于是有-
,于是有-![]() 由
由![]() 是基础解系,故线性无关,所以
是基础解系,故线性无关,所以![]() 。于是
。于是![]() ,但
,但![]() ,所以
,所以![]() 所以
所以![]() 线性无关。
线性无关。

