当前位置:课程学习>>第五章 矩阵>>学习内容>>视频课堂>>知识点二
知识点二:矩阵的运算
现在我们来定义矩阵的运算,它们可以认为是矩阵之间一些最基本的关系. 下面要定义的运算时矩阵的加法、乘法、矩阵与数的乘法以及矩阵的转置.
为了确定起见,我们取定一个数域![]() ,以下所讨论的矩阵全是由数域
,以下所讨论的矩阵全是由数域![]() 中的数组成的.
中的数组成的.
![]() .加法
.加法
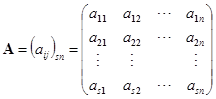 ,
,
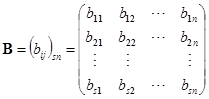
是两个![]() 矩阵,则矩阵
矩阵,则矩阵
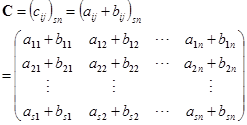
称为![]() 和
和![]() 的和,记为
的和,记为
![]() .
.
矩阵的加法就是矩阵对应的元素相加. 当然,相加的矩阵必须有相同的行数和列数. 由于矩阵的加法归结为它们的元素的加法,也就是数的加法,所以,不难验证,它有
结合律:![]() ;
;
交换律:![]() .
.
元素全为零的矩阵称为零矩阵,记为![]() ,在不致引起混乱的时候,可简单地记为
,在不致引起混乱的时候,可简单地记为![]() . 显然,对所有的
. 显然,对所有的![]() ,
,
![]() .
.
矩阵
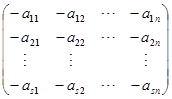
称为矩阵![]() 的负矩阵,记为
的负矩阵,记为![]() . 显然有
. 显然有
![]() .
.
矩阵的减法定义为
![]() .
.
例 在§![]() 我们看到,某一种物资如果有
我们看到,某一种物资如果有![]() 个产地,
个产地,![]() 个销地,那么一个调运方案就可表示为一个
个销地,那么一个调运方案就可表示为一个![]() 矩阵,矩阵中元素
矩阵,矩阵中元素![]() 表示由产地
表示由产地![]() 要运到销地
要运到销地![]() 的这种物资的数量,比如说吨数. 如果从这些产地还有另一种物资要运到这些销地,那么,这种物资的调运方案也可表示为一个
的这种物资的数量,比如说吨数. 如果从这些产地还有另一种物资要运到这些销地,那么,这种物资的调运方案也可表示为一个![]() 矩阵.于是从产地到销地的总的运输量也表示为一个矩阵. 显然,这个矩阵就等于上面两个矩阵的和.
矩阵.于是从产地到销地的总的运输量也表示为一个矩阵. 显然,这个矩阵就等于上面两个矩阵的和.
根据矩阵加法的定义应用关于向量组的秩的性质,很容易看出秩![]() 秩
秩![]() +秩
+秩![]()
![]() .乘法
.乘法
再给出乘法定义之前,我们先看一个引出矩阵乘法的问题.
设![]() 和
和![]() 是两组变量,它们之间的关系为
是两组变量,它们之间的关系为
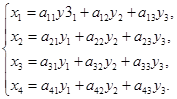
![]()
又如![]() 是第三组变量,它们与
是第三组变量,它们与![]() 的关系为
的关系为
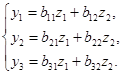
![]()
由![]() ,
,![]() 不难看出
不难看出![]() 与
与![]() 的关系:
的关系:
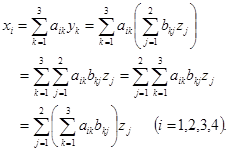
![]()
如果我们用
![]()
![]()
![]()
来表示![]() 与
与![]() 的关系,比较
的关系,比较 ![]() ,
,![]() ,就有
,就有
![]()
![]()
![]()
用矩阵的表示法,我们可以说,如果矩阵
![]() ,
,![]()
分别表示变量![]() 与
与![]() 以及
以及![]() 之间的关系,那么表示
之间的关系,那么表示![]() 与
与![]() 之间关系的矩阵
之间关系的矩阵
![]()
就由公式![]() 决定. 矩阵
决定. 矩阵![]() 称为矩阵
称为矩阵![]() 与
与![]() 的乘积,记为
的乘积,记为
![]()
一般地,我们有:
定义 ![]() 设
设
![]() ,
,![]() ,
,
那么矩阵
![]() ,
,
其中
![]() ,
, ![]()
称为![]() 与
与![]() 的乘积,记为
的乘积,记为
![]() .
.
由矩阵乘法的定义可以看出,矩阵![]() 与
与![]() 的乘积
的乘积![]() 的第
的第![]() 行第
行第![]() 列的元素等于第一个矩阵
列的元素等于第一个矩阵![]() 的第
的第![]() 行与第二个矩阵
行与第二个矩阵![]() 的第
的第![]() 列的对应元素乘积的和. 当然,在乘积的定义中,我们要求第二个矩阵的行数与第一个矩阵的列数相等.
列的对应元素乘积的和. 当然,在乘积的定义中,我们要求第二个矩阵的行数与第一个矩阵的列数相等.
例 ![]() 设
设
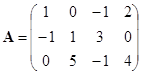 ,
,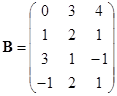 ,
,
那么
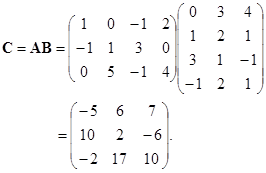
乘积的矩阵中各个元素是根据公式![]() 得出的,例如,第二行第一列的元素
得出的,例如,第二行第一列的元素![]() 是矩阵
是矩阵![]() 的第二行元素与矩阵
的第二行元素与矩阵![]() 的第一列对应元素乘积之和:
的第一列对应元素乘积之和:
![]() .
.
其余可类似得到.
例 ![]() 如果
如果
![]()
是一线性方程组的系数矩阵,而
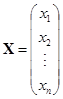 ,
,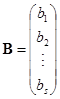
分别是未知量和常数项所成的![]() 和
和![]() 矩阵,那么线性方程组就可以写成矩阵的等式
矩阵,那么线性方程组就可以写成矩阵的等式
![]() .
.
例 ![]() 在空间中作一坐标系的转轴. 设由坐标系
在空间中作一坐标系的转轴. 设由坐标系![]() 到
到![]() 的坐标变换的矩阵为
的坐标变换的矩阵为
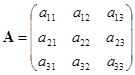 ,
,
如果令
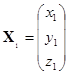 ,
,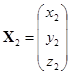 ,
,
那么坐标变换的公式可以写成
![]() .
.
如果再作一次坐标系的转轴,设由第二个坐标系![]() 到第三个坐标系
到第三个坐标系![]() 的坐标变换公式为
的坐标变换公式为
![]() ,
,
其中
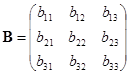 ,
,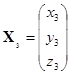 .
.
那么不难看出,由第一个坐标系到第三个坐标系的坐标变换的矩阵即为
![]() .
.
矩阵的乘法适合结合律. 设
![]() ,
,![]() ,
,![]() ,
,
我们证明
![]() .
.
令
![]() ,
,![]() ,
,
其中
![]()
![]() ,
,
![]()
![]() .
.
因为
![]()
中![]() 的第
的第![]() 行第
行第![]() 列元素为
列元素为
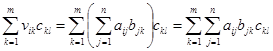 ,
, ![]()
而
![]()
中![]() 的第
的第![]() 行第
行第![]() 列元素为
列元素为
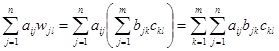 ,
, ![]()
由于双重连加号可以交换次序,所以![]() 与
与![]() 的结果是一样的,这就证明了结合律.
的结果是一样的,这就证明了结合律.
但是,矩阵的乘法不适合交换律,即一般说来,
![]() .
.
这是由于,一方面在乘积中要求第一个因子的列数等于第二个因子的行数,否则没有意义. 所以,当![]() 有意义时,
有意义时,![]() 不一定有意义. 另一方面即使
不一定有意义. 另一方面即使![]() 与
与![]() 都有意义,它们的级数也不一定相等,因为乘积的行数等于第一个因子的行数,列数等于第二个因子的列数. 如上面例
都有意义,它们的级数也不一定相等,因为乘积的行数等于第一个因子的行数,列数等于第二个因子的列数. 如上面例![]() 中,
中,![]() 是一
是一![]() 矩阵,而
矩阵,而![]() 是一
是一![]() 矩阵. 即使相乘的矩阵都是
矩阵. 即使相乘的矩阵都是![]() 矩阵,这时,
矩阵,这时,![]() 与
与![]() 都有意义,而且都是
都有意义,而且都是![]() 矩阵,但它们也不一定相等. 例如,
矩阵,但它们也不一定相等. 例如,
![]() ,
, ![]() ,
,
![]() ,
,
而
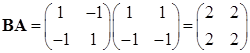 .
.
在这个例子中我们还看到,两个不为零的矩阵的乘积可以是零,这是矩阵乘法的一个特点. 由此还可得出矩阵乘法的消去律不成立. 即当![]() 时不一定有
时不一定有![]() . 读者由上面的例子的启发可以举出类似的例子.
. 读者由上面的例子的启发可以举出类似的例子.
定义 ![]() 主对角线上的元素全是
主对角线上的元素全是![]() ,其余元素全是
,其余元素全是![]() 的
的![]() 矩阵
矩阵
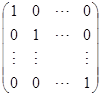
称为![]() 级单位矩阵,记为
级单位矩阵,记为![]() ,或者在不致引起含混的时候简单写为
,或者在不致引起含混的时候简单写为![]() . 显然有
. 显然有
![]() ,
,
![]() .
.
矩阵的乘法和加法还适合分配律,即
![]() ,
, ![]()
![]() .
. ![]()
这两个式子的证明留给读者自己来作. 应该指出,由于矩阵的乘法不适合交换律,所以![]() 与
与![]() 是两条不同的规律.
是两条不同的规律.
我们还可以定义矩阵的方幂. 设![]() 是一
是一![]() 矩阵,定义
矩阵,定义
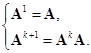
换句话说,![]() 就是
就是![]() 个
个![]() 相乘. 当然,方幂只能对行数与列数相等的矩阵来定义. 由乘法的结合律,不难证明
相乘. 当然,方幂只能对行数与列数相等的矩阵来定义. 由乘法的结合律,不难证明
![]() ,
,
![]() ,
,
这里![]() ,
,![]() 是任意正整数. 证明留给读者去做. 因为矩阵乘法不适合交换律,所以
是任意正整数. 证明留给读者去做. 因为矩阵乘法不适合交换律,所以![]() 与
与![]() 一般不相等.
一般不相等.
![]() .数量乘法
.数量乘法
定义 ![]() 矩阵
矩阵
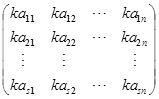
称为矩阵![]() 与数
与数![]() 的数量乘积,记为
的数量乘积,记为![]() . 换句话说,用数
. 换句话说,用数![]() 乘矩阵就是把矩阵的每个元素都乘上
乘矩阵就是把矩阵的每个元素都乘上![]() .
.
不难验证,数量乘积适合以下的规律:
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
. ![]()
我们只证明等式![]() ,其余留给读者证明. 设
,其余留给读者证明. 设
![]() ,
,![]() ,
,
在![]() ,
,![]() ,
,![]() 中,
中,![]() 的元素依次为
的元素依次为
今后![]() 表示第
表示第![]() 行第
行第![]() 列交叉处的位置.
列交叉处的位置.
![]() ,
,
![]() ,
,
![]() .
.
显然它们是一样的,这就证明了等式![]() .
.
矩阵
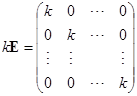
通常称为数量矩阵. 作为![]() 的特殊情形,如果
的特殊情形,如果![]() 是一
是一![]() 矩阵,那么有
矩阵,那么有
![]() .
.
这个式子说明,数量矩阵与所有的![]() 矩阵作乘法是可交换的.
矩阵作乘法是可交换的.
可以证明:如果一个![]() 级矩阵与所有的
级矩阵与所有的![]() 级矩阵作乘法是可交换的. 那么这个矩阵一定是数量矩阵(参看习题
级矩阵作乘法是可交换的. 那么这个矩阵一定是数量矩阵(参看习题![]() ). 再有,
). 再有,
![]() ,
,
![]() ,
,
这就是说,数量矩阵的加法与乘法完全归结为数的加法与乘法.
![]() .转置
.转置
把一矩阵![]() 的行列互换,所得到的矩阵称为
的行列互换,所得到的矩阵称为![]() 的转置,记为
的转置,记为![]() . 可确切地定义如下:
. 可确切地定义如下:
定义 ![]() 设
设
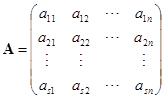 ,
,
所谓![]() 的转置就是指矩阵
的转置就是指矩阵
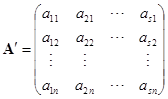 .
.
显然,![]() 矩阵的转置是
矩阵的转置是![]() 矩阵.
矩阵.
矩阵的转置适合以下的规律:
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
. ![]()
![]() 表示两次转置就还原,这是显然的.
表示两次转置就还原,这是显然的. ![]() ,
,![]() 也很容易验证.现在来看一下
也很容易验证.现在来看一下![]() . 设
. 设
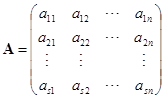 ,
, 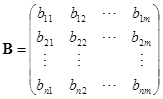 .
.
![]() 中
中![]() 的元素为
的元素为
![]() ,
,
所以![]() 中
中![]() 的元素就是
的元素就是
![]() .
. ![]()
其次,![]() 中
中![]() 的元素是
的元素是![]() ,
,![]() 中
中![]() 的元素是
的元素是![]() ,因之,
,因之,![]() 中
中![]() 的元素即为
的元素即为
![]() .
. ![]()
比较![]() ,
,![]() 即得
即得![]() .
.
例 设
![]() ,
,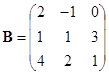 .
.
于是
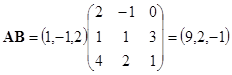 ,
,
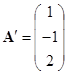 ,
,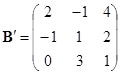
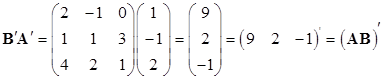 .
.
