这一节我们来看一下矩阵乘积的行列式与秩和它的因子的行列式与秩的关系.

关于乘积的行列式有：

定理   设 ，是数域上的两个矩阵 ，那么

，                           

即矩阵乘积的行列式等于它的因子的行列式的乘积.

证明  这是第二章第八节中已经证明了的结论.

用数学归纳法，定理不难推广到多个因子的情形，即有

推论  设，，，是数域上的矩阵 ，于是.

定义   数域上的矩阵称为非退化的，如果；否则称为退化的.

显然，一矩阵是非退化的充分必要条件是它的秩等于.

从定理，立刻推出：

推论   设，是数域上矩阵 ，矩阵为退化的充分必要条件是，中至少有一个是退化的.

关于矩阵乘积的秩，我们有：

定理   设是数域上的矩阵，是数域上矩阵，于是

秩[秩，秩]，                 

证明  为了证明，只需要证明秩秩，同时秩秩. 现在来分别证明这两个不等式.

设

， .

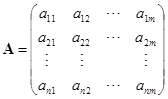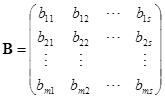令，，，表示的行向量，，，，表示的行向量. 由计算可知，的第个分量和的第个分量都等于，因而

，

即矩阵的行向量组，，，可经的行向量组线性表出. 所以得秩不能超过的秩（参见第三章习题），也就是说，

秩秩.

同样，令，，，表示的列向量，，，，表示的列向量. 由计算可知

         .

这个式子表明，矩阵的列向量组可以经矩阵的列向量组线性表出，因而前者的秩不可能超过后者的秩，这就是说，

秩秩.

用数学归纳法，定理不难推广到多个因子的情形，即有

推论   如果，那么

秩秩.