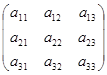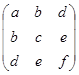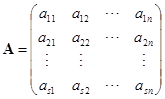在线性方程组的讨论中我们看到，线性方程组的一些重要性质反映在它的系数矩阵和增广矩阵的性质上，并且解方程组的过程也表现为变换这些矩阵的过程. 除线性方程组之外，还有大量的各种各样的问题也都提出矩阵的概念，并且这些问题的研究常常反映为有关矩阵的某些方面的研究，甚至于有些性质完全不同的、表面上完全没有联系的问题，归结成矩阵问题以后却是相同的. 这就使矩阵成为数学中一个极其重要的应用广泛的概念，因而也就使矩阵成为代数特别是线性代数的一个主要研究对象. 这一章的目的是引入矩阵的运算，并讨论它们的一些基本性质.

为了使读者对矩阵的概念以及下面要讨论的问题的背景有些了解，我们来介绍一些提出矩阵概念的问题. 当然，由于篇幅和目前知识的限制，介绍的方面有很大的局限性.

.在解析几何中考虑坐标变换时，如果只考虑坐标系的转轴（反时针方向转轴），那么平面直角坐标变换的公式为

                  

其中为轴与轴的夹角. 显然，新旧坐标之间的关系，完全可以通过公式中系数所排成的矩阵

                      

表示出来. 通常，矩阵称为坐标变换的矩阵. 在空间情形，保持原点不动的仿射坐标系的变换有公式

                   

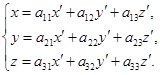
同样，矩阵

                     

就称为坐标变换的矩阵.

.二次曲线的一般方程为

 

            

的左端可以用表

来表示，其中每一个数就是它所在的行和列所对应的，或的乘积的系数，而的左端就是按这样的约定所形成的项的和. 换句话说，只要规定了，，的次序，二次方程的左端就可以简单地用矩阵

                   

来表示. 通常，称为二次曲线的矩阵. 以后我们会看到，这种表示法不止是形式上的. 事实上，矩阵的行列式就是解析几何中二次曲线的不变量，这表明了矩阵的性质确实反映了它所表示的二次曲线的性质.

.在讨论国民经济的数学问题中也常常用到矩阵. 例如，假设在某一地区，某一种物资，比如说媒，有个产地和个销地，那么一个调运方案就可用一个矩阵

来表示，其中表示由产地运到销地的数量.

.维向量也可以看成矩阵的特殊情形. 维行向量就是矩阵，维列向量就是矩阵.

以后我们用大写的拉丁字母，，，或者，，

来表示矩阵.

有时候，为了指明所讨论的矩阵的级数，可以把矩阵写成，，，或者

，，

（注意矩阵的符号与行列式的符号的区别）.

设，，如果，，且，对；

都成立，我们就说. 即只有完全一样的矩阵才叫做相等.