在§我们看到，矩阵与复数相仿，有加、减、乘三种运算. 矩阵的乘法是否也和复数一样有逆运算呢？这就是本节所要讨论的问题.

这一节讨论的矩阵，如不特殊说明，都是矩阵.

我们知道，对于任意的级方阵都有

，

这里是级单位矩阵. 因之，从乘法的角度来看，级单位矩阵在级方阵中的地位类似于在复数中的地位. 一个复数的倒数可以用等式

来刻画，相仿地，我们引入：

定义   级方阵称为可逆的，如果有级方阵，使得

，                         

这里是级单位矩阵.

首先我们指出，由于矩阵的乘法规则，只有方阵才能满足（读者自己证明）. 其次，对于任意的矩阵，适合矩阵的矩阵是唯一的（如果有的话）. 事实上，假设，是两个适合的矩阵，就有

.

定义   如果矩阵适合，那么就称为的逆矩阵，记为.

下面要解决的问题是：在什么条件下矩阵是可逆的？如果可逆，怎样求？

定义   设是矩阵

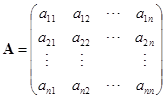
中元素的代数余子式，矩阵

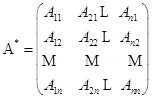
称为 的伴随矩阵.

由行列式按一行（列）展开的公式立即得出：

，                     

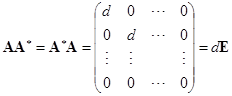其中.

如果，那么有得

.                          

定理   矩阵是可逆的充分必要条件是非退化，而

  .

证明  当，由可知，可逆，且

.                                 

反过来，如果可逆，那么有使

.

两边取行列式，得

,                              

因而，即非退化.

根据定理容易看出，对于级方阵，，如果

，

那么，就都是可逆的并且它们互为逆矩阵.

定理不但给出了一矩阵可逆的条件，同时也给出了求逆矩阵的公式. 按这个公式来求逆矩阵，计算量一般是非常大的. 在以后我们将给出另一种求法.

由可以看出，如果，那么

.

推论  如果矩阵，可逆，那么与也可逆，且

，

.

证明  由定理即得推论的前一半，现在来证后一半. 由

两边取转置，有

，

因之

.

由

即得

.

利用矩阵的逆，可以给出克拉默法则的另一种推导法. 线性方程组

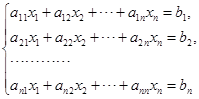
可以写成（§例）

.                             

如果，那么可逆.用

.

代入，得恒等式，这就是说是一个解.

如果

是的一个解，那么由

得

，

即   

.

 

这就是说，解是唯一的. 用的公式代入，乘出来就是克拉默法则中给出的公式.

联系到可逆矩阵，关于矩阵乘积的秩有：

定理   是一个矩阵，如果是可逆矩阵，是可逆矩阵，那么

秩=秩=秩.

证明  令

,

由定理，

秩秩；

但是由

，

又有

秩秩.

所以

秩=秩=秩.

另一个等式可以同样的证明.