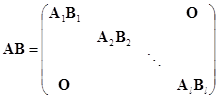这一节，我们来介绍一下在处理级数较高的矩阵时常用的方法，即矩阵的分块. 有时候，我们把一个大矩阵看成是由一些小矩阵组成的，就如矩阵是由数组成的一样. 特别在运算中，把这些小矩阵当成数一样来处理. 这就是所谓矩阵的分块.

为了说明这个方法，下面看一个例子. 在矩阵

中，表示级单位阵，而

，.

在矩阵

中，

，，

，.

在计算时，把，都看成是由这些小矩阵组成的，即按级矩阵来运算. 于是

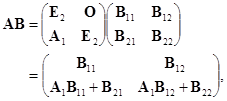
其中

    

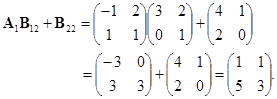
因之

.

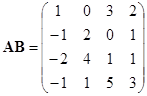不难验证，直接按级矩阵乘积的定义来作，结果是一样的.

一般地说，设，，把，分成一些小矩阵：

，                       

 

，                        

其中每个是小矩阵，每个是小矩阵. 于是有

，                       

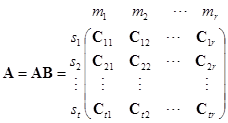其中

                  

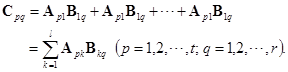
这个结果由矩阵乘积的定义直接验证即得，就不详细说明了.

应该注意，在分块矩阵，中矩阵的列的分法必须与矩阵的行的分法一致.

以下会看到，分块乘法有许多方便之处. 常常在分块之后，矩阵间相互的关系看得更清楚.

实际上，在证明关于矩阵乘积的秩的定理时，我们已经用矩阵分块的想法. 在那里，用，，，表示的行向量，于是

，

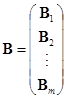这就是的一种分块. 按分块相乘，就有

.

用这个式子很容易看出的行向量是的行向量的线性组合；将进行另一种分块乘法，从结果中可容易看出的列是的列的线性组合（读者自己做一下）

作为另一个例子，我们来求矩阵

的逆矩阵，其中，分别是级和级的可逆矩阵，是矩阵，是零矩阵.

首先，因为

，

所以当，可逆时，也可逆. 设

，

于是

，

这里，分别表示级和级单位矩阵. 乘出并比较等式两边，得

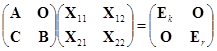由第一、二式得

，，

代入第四式，得

，

代入第三式，得

，.

因此

.

特别地，当时，有

.

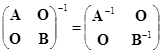形式为

的矩阵，其中是数，通常称为对角矩阵，而形式为

的矩阵，其中是矩阵，通常称为准对角矩阵. 当然，准对角矩阵包括对角矩阵作为特殊情形.

对于有两个相同分块的准对角矩阵

，，

如果它们相应的分块是同级的，那么显然有

，

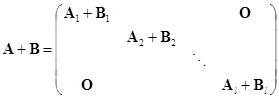
它们还是准对角矩阵.

其次，如果，，，都是可逆矩阵，那么

.
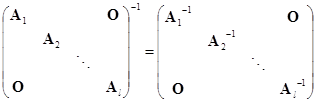
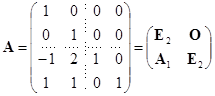
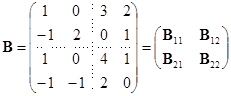
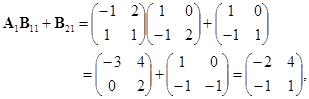
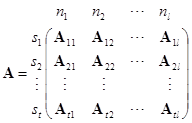
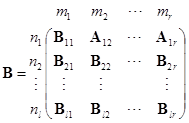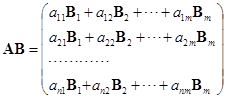
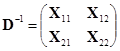
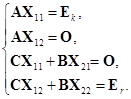
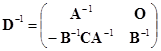
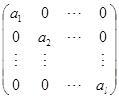
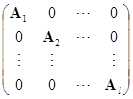
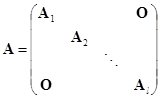
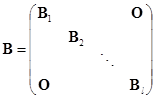