当前位置:课程学习>>第五章 矩阵>>课前准备>>本章导学
本章概述
矩阵是线性代数中的重要内容,线性代数中的计算及应用都离不开矩阵及其计算。掌握并灵活运用矩阵运算规律是非常重要的。矩阵理论许多内容都离不开线性方程组的联系,求解线性方程组的过程实质就是矩阵计算,应该把它们联系起来学习。矩阵的分块技巧,在矩阵理论研究中非常重要,但处理问题时比较灵活,只有多训练才能掌握。
学习目标
要求:重点掌握矩阵的乘法运算及其性质,可逆矩阵的求法。
1.掌握矩阵运算,特别是乘法运算。
2.了解一些特殊矩阵和矩阵乘积的秩矩阵。
3.掌握求逆阵的方法。
4.了解矩阵分块的概念。
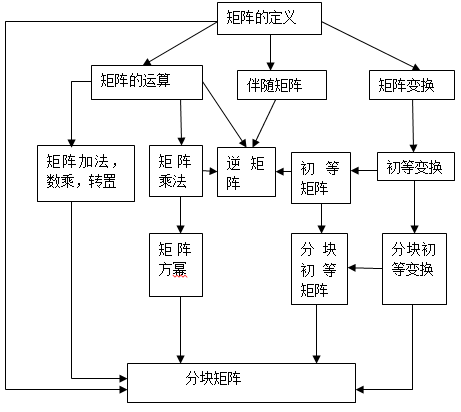
知识结构框图
重点难点解析与学习建议
本章重点是掌握矩阵的运算以及它们的运算规律。由于矩阵运算和熟知的数的运算规律有些是相同的,但也有许多不同之处,这些不同之处正是易犯错误的地方。
伴随矩阵![]() 是为计算逆矩阵而引人的,但在具体求逆矩阵时,只对低级矩阵(特别是2级矩阵)采用伴随矩阵法进行计算,对2级以上矩阵利用初等变换法求逆矩阵更方便。在涉及伴随矩阵的有关计算及证明时,往往利用伴随矩阵的基本公式
是为计算逆矩阵而引人的,但在具体求逆矩阵时,只对低级矩阵(特别是2级矩阵)采用伴随矩阵法进行计算,对2级以上矩阵利用初等变换法求逆矩阵更方便。在涉及伴随矩阵的有关计算及证明时,往往利用伴随矩阵的基本公式![]() ,来推证及化简。
,来推证及化简。
利用初等矩阵及分块初等矩阵可以将对矩阵的初等变换和分块矩阵的分块初等变换转化成矩阵的乘法运算,对于解决一些涉及矩阵理论和计算题很有用,但推证过程有一定技巧,需要不断训练总结。
有关矩阵的秩的等式或不等式的证明,常常和向量组的秩,线性方程组的解等相联系,推证有一定的难度。熟记关于矩阵的秩的一些结论,对有关问题的论证会有很大的帮助。
课前提问
1、你能写出矩阵乘法定义吗?,并举一个例子。
2、矩阵乘法都有哪些性质?哪些性质与数的乘法不同?
3、矩阵乘积的矩阵与秩有哪些性质?请写出。
4、 给出矩阵逆的定义,并给出求逆矩阵的公式?
5、举例说明矩阵的分块,并且举例说明矩阵分块乘法的运算?
6、给出初等矩阵的定义,初等矩阵的性质?
7、总结分块乘法的初等变换的用法,并注意应用?
8、你认为这一章中的哪些实例或者练习题最有意思?哪些题目感觉较难,作为笔记的内容之一,试着总结一下.

