一、量子论和光子学说

1900年，为了解释黑体辐射实验现象，Planck引进了一个崭新的不连续性概念，即量子化的概念。物体吸收或发射电磁辐射，只能以“量子”的方式进行，每个“量子”的能量为e＝hn。从经典力学来看，这种能量不连续的概念是完全不能被允许的，但恰恰很好地解释了黑体辐射能量密度随频率变化的实验事实。

光电效应是光照在金属表面上，金属发射出电子的现象，也称光致电离。这种因光的作用而产生的电子称为光电子，由光电子形成的电流叫光电流。根据光波的经典理论，波的能量与它的强度成正比，而与频率无关。因此只要有足够的强度，任何频率的光都能产生光电效应，而电子的动能将随着光强的增加而增加，与光的频率无关，这些经典物理学家的推测不符。显然，对于光电效应的实验事实，应用经典的电磁波理论得到的却是与实验事实相反的结论。

1905年， A. Einstein 依据 Planck 的能量子的思想，提出了光子学说，成功地解释了光电效应的实验结果，不仅很大程度支持了Planck的能量子观点，而且也指出了光具有粒子性质。

光子学说认为：

(1) 光的能量是不连续的，也是量子化的，最小能量单位称为光量子，简称光子。光子的能量为： e＝hn    

(2) 光为一束以光速c 运动的光子流，其强度I 正比于单位体积内光子的数目即光子的密度，   

(3) 光子不但有能量，还有质量m。根据质能联系定律，光子的质量m为：

              

值得注意的是，光子虽然有质量，却没有静止质量m0，因为根据相对论原理，

     

对于光子，所以m0必定为0，即光子没有静止质量。

(4) 光子既然有质量，就必然有动量

=                

(5) 光子与电子碰撞时服从能量守恒和动量守恒定律。

根据光子学说，Einstein提出了解释光电效应的光电方程：

               

1913年，N. Bohr在解释原子线光谱的实验事实时，提出了氢原子结构的Bohr模型, 认为原子在电子轨道上运动时，角动量 M是不连续的，也是量子化的。

        

同时指出原子存在于一些分立能值的稳定状态，简称为定态。其中，能量最低的定态为基态，其余为激发态。处于定态的原子不发射能量，从一个定态（E1）跃迁到另一个定态（E2）时，原子会发射或吸收辐射能，其频率满足于：

     

根据Bohr原子结构论，可以求得氢原子的电子轨道能级和轨道半径等，当时不仅成功地解释了氢原子的实验上观察到的三个谱线系，而且还预测了氢原子光谱中可能存在的另一个线系，即1915年T. Lyman在远紫外区找到的线系，现在称之为Lyman系。Bohr理论的伟大之处在于第一次将量子论用于原子结构，不但成功地解释了氢原子光谱，而且还解释了类氢离子（例如He+, Li2+）的光谱现象。基于Bohr对量子论和原子结构的突出贡献，1922年他荣获了诺贝尔物理学奖，从此也掀开了量子力学发展的篇章。

二、波粒二象性

在经典物理学中，粒子就是粒子，波就是波，粒子和波各自遵循不同的运动规律：粒子服从Newton运动方程，波服从Maxwell波动方程。所谓粒子性，一般是指一个客体具有质量、电荷等性质。所谓波动性，一般是指实际的物理量空间分布呈周期性变化，并有干涉和衍射现象。然而，按照经典物理学的观点却无法解释光电效应的实验事实，让人们感受到粒子和波之间存在着某些必然的联系。

事实上，相对论将质量和能量相联系，得到E=mc2；而 Planck 和 Einstein又将能量和频率相联系，即。 两者结合起来就给出了质量与频率间的关系，即

这就是说，任何质量为m的物质，也和光一样具有波动性，其波长为：

            

其中为物质波的波长，为粒子的动量，h为Planck常数。这就是著名的de Broglie关于物质波（或称de Broglie波）的假设，又被称作de Broglie关系式。显然，具有能量E和动量p的粒子与一个波相当。如果物质波的存在被证实，说明实物粒子也具备波粒二象性。

1927年，在贝尔实验室工作的 C. J. Davisson和 L. H. Germer发现了电子衍射现象：如图1.1-1所示，高能电子流从A处射出，通过薄的镍单晶B（作为光栅）的晶格狭缝射到感光屏C上，观察散射电子束的强度和散射角a的关系，结果得到了与单色光通过小圆孔时得到的图象完全类似的明暗相间的衍射图象。

 

图1.1-1 电子衍射示意图

证实电子具有波动性的另一个实验工作来自 G. P. Thomson 所完成的多晶体电子衍射实验。他用电子束穿过金属薄片，发现电子入射到金属晶体上产生的衍射条纹与光入射到晶体上产生衍射条纹完全一样（图1.1-2）。

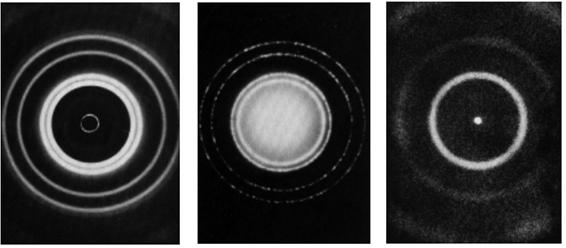
(a)             (b)            (c)
图1.1-2    ( a )X射线通过铝箔所得到的衍射环
        ( b )电子束通过铝箔所得到的衍射环
        ( c )中子束通过铜箔所得到的衍射环

1932 年， O. Stern 用氢和氦分子做实验，同样也观测到了衍射现象，这就进一步证实了实物微粒具有波动性，而不仅限于电子，其它一切微观粒子如原子、分子、质子、中子、α粒子等也都有类似的波动性，有力地证实了 de Broglie假说。因此说波粒二象性是一切物质所具有的普遍属性，而实物微粒具有波动性被称作物质波。

三、不确定关系

由于微观粒子具有波动性，我们只能说在某一时刻某个地方它是否具有出现的几率或机会，至于是否真的在那个地方出现却不得而知，因而它没有确定的运动轨道，即在某一时刻微观粒子的坐标和动量不能同时确定。

1927年，海森堡（W.Heisenberg）经过对德布罗意关系式和一些实验的分析探讨，提出了如下不确定关系式：

              

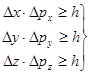
其中是位置的测不准量，是动量的测不准量。测不准关系表明，对于微观粒子的位置描述的越准确（即位置的测不准量越小），其动量的描述就越不准确（即动量的测不准量就越大），反之，动量的描述越准确，位置的描述就越不准确。