一、波函数

量子力学基本假设1：微观粒子的运动状态可以用一个波函数描述。

例如一个粒子的体系，其波函数为；三个粒子的体系，其波函数为，不含时间的波函数称为定态波函数，是原子和分子中电子状态的最可能类型，也是本书将要重点展开叙述与讨论的函数。

1926年，M. Born 提出描述电子等实物粒子的运动状态的波函数的统计解释。他认为空间任何一点上波的强度（即振幅绝对值的平方）和粒子出现的概率成正比。按照这种解释描述的粒子的波称为概率波，所以通常将用波函数描述的物质波称为概率波。

由于空间某点波的强度与波函数模的平方成正比，其中，即在该点附近找到粒子的概率正比于。在原子、分子等体系中，称为概率密度，它就是通常所说的电子云；而为空间某点附近体积元中电子出现的概率。

通常若，则波函数ψ被称为归一化波函数，即波函数是归一化的。对于没有归一化的波函数，只要是平方可积的，就可以乘上一个合适的因子c使之归一化。

，   

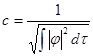
通常称作波函数的归一化条件，c为归一化常数。

事实上，并不是所有的函数形式都可以描述微观粒子的运动状态。只有符合下面三个条件的波函数才可以用来描述微观粒子的运动状态，这样的波函数也被称作合格波函数。

（1）描述微观粒子运动状态的波函数首先必须是单值的，因为当波函数ψ在空间每一点只有一个值时，波函数模的平方才能具备单值性；

（2）波函数ψ必须是连续的，而且ψ对坐标（x，y，z）进行求一级导数后，所获得的新函数也应该是连续的函数；

（3）波函数ψ模的平方必须是可积的，也就是有限的。

上述三个条件——单值、连续、平方可积或有限是判断合格波函数的基本条件。

二、力学量和算符

量子力学基本假设2：量子力学每一可观测物理量都对对应一线性厄米算符。

所谓力学量，是指位置、速度、动量、角动量、能量等动力学变量，这些力学量不仅在经典力学中经常用到，在量子力学中也经常使用和讨论，并且都是体系可观测的性质。

（1）算符实际上就是一种运算符号。若某一种运算符号可以把函数u变成为函数v，可表示为

          

则表示这种运算的符号就称为算符。

例如，就是算符，它表示对一个函数u进行导数运算；假设xu=v， x也是算符,它对u的作用是与u相乘；假设数字3是一个算符，表示对某函数乘以数字3，例如也是算符，它表示对函数u取平方根。

（2）设 u1和u2是两个任意函数，它们的线性组合函数为 c1u1+c2u2, 其中c1和c2为任意常数，如果某算符与线性组合函数c1u1+c2u2,满足

       

则称为线性算符。即两个函数的任意线性组合，经算符作用后，仍然得到两个新函数的线性组合，则该算符叫线性算符。

（3）对于算符，存在复共轭算符，是把算符中的i改为-i。

如果线性算符和它的复共轭算符满足下面的关系

              

其中u1和u2是任意两个平方可积的函数，积分遍于自变量的全部区间，则称是厄米算符。如果一个算符既是线性算符又是厄米算符，称该算符为线性厄米算符。

（4）本征函数和本征值

假如某函数被力学量算符作用的结果就是在原来的函数上乘以某常数，则说函数是算符属于本征值的本征函数：

              

通常本征值也称作这个力学量的确定值。相应的方程称为本征方程。

（5）对于任意一个量子力学体系，它的每一个可观测力学量都与一个线性厄米算符相对应。每一个可观测力学量可以是能量、坐标、动量、时间等，量子力学将物理量写成算符的过程称作算符化过程，提出了下列算符化规则：

时空坐标算符和常数算符就是它们自身，即：

           

约定动量分量算符为：

         

任意一个力学量（L）的算符形式可按下列步骤得到：

首先，写出该力学量在经典力学中的时空坐标和动量描述的表达式 L=L(x ,y ,z ,Px ,Py ,Pz , t)，然后，将表达式中的动量换成动量算符，由于时空坐标算符就是它们自身，即可得到力学量L的算符

通常能量算符被记作，称作Hamilton算符，它等于动能算符和势能算符的和，可以表述为：

      

对于在三维空间运动的体系，能量的经典表达式和能量算符分别为：

     

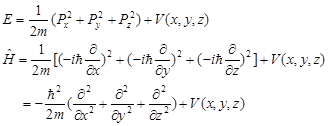
令，叫Laplace算符，将代入三维空间运动的体系能量算符，则：

     

微观粒子的运动方程

量子力学基本假设3：微观粒子运动满足薛定谔方程。

由于体系总能量E是势能V和动能之和，即

          

          

假如粒子仅在一维x方向运动，则变形为：

    

这就是质量为m的粒子在一维x方向运动所满足的定态Schrödinger方程。

所谓定态是指体系的势能项V不含时间变量t，体系的势能不随时间变化，换句话说即体系的Hamilton量不随时间变化，这种状态称为定态。当体系的哈密顿算符不显含时间变量时，能量算符的本征方程：

         

在三维空间 (x, y, z) 运动的定态Schrödinge方程是：

 ，       

应当注意，不要对定态这个概念发生误解，不能理解为处于定态的粒子是静止的，定态是指（概率密度）值不随时间而改变。

四、态叠加原理

量子力学基本假设4：微观粒子运动满足态叠加原理。

若波函数（i=1,2,3……n）分别描述体系的n个可能的运动状态，那么它们线性叠加后得到的波函数仍然代表体系的一个可能的运动状态。这在量子力学中被称作态叠加原理。

，  

五、关于自旋

量子力学基本假设5：微观粒子除了做空间运动外，还做自旋运动。

将在第二章讲解。