一、势箱中运动的粒子

（1）所谓一维势箱，就是指粒子的坐标x被限定在0和之间，指粒子运动的势能在一线段内为零，其余各处势能均为无限大，表明粒子不可能出现在一维势箱之外，如图1.3-1。这种体系在物理学上看来似乎是不实际的，但作为一种近似，在讨论金属与共轭分子中电子的运动时，都可应用这种模型。

在Ⅰ、Ⅲ区域中，, V=∞，粒子不可能出现在此处，表明粒子出现的概率为零（=0），说明波函数等于零，因此ψ为零，即ψI=0或 ψⅢ=0。

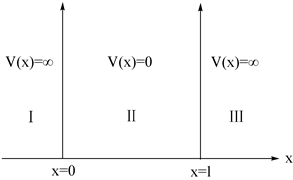
图 1.3-1  一维势箱粒子的势能

在Ⅱ区域中，0<x<, V=0，这时Schrödinger方程为

              

可以看出上式是常系数的线性齐次二阶微分方程。该方程在数学上存在一个通解，

           

式中A, B为任意两个待定系数，能量E也待确定。

对于一个微观体系，求得Schrödinger方程通解后，还要确定满足体系特定条件的特解。在一维势箱中，体系的特定条件是箱外波函数等于零。根据波函数的连续性，则在边界上（x=0，x=处）波函数也应为零，即，。

在x=0处，

即利用此边界条件，可以确定常数A恒等于零，故，

           

同样，利用在边界x=处的连续性条件，得

           

显然，均满足条件。但是B不能等于0，因为A, B同时都为零会导致波函数在各处均等于零，即在一维箱子中找不到粒子，等于是一只空箱子，与题意产生矛盾，所以要使上式成立，必须

  

因此        

习惯上，n只取正整数，因为取负整数并没有给出能量 E的新结果。显然能量E与n有关，n称为量子数，故能量通常记作。

 

将能量表达式代入方程得到：

  

显然也受量子数n的决定，所以可记作，。在此波函数中，待定系数B如果确定了，则波函数就被唯一确定。

描述微观粒子运动的状态函数具有归一化性质，所以利用归一化条件可以确定常数B。

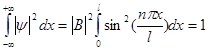
所以，习惯上取, 这样，描述一维势箱中运动的粒子的波函数即为：

  

（2）关于能量

由能量公式可知，粒子的能量只能取分立的数值，被称为能级。例如，，，，能量最低的状态称为基态，而且称这个能量最低的状态ψ1所具有的能量叫零点能，能量较高的状态为激发态，状态依次称为第一和第二激发态。

相邻两个能级之间的差值被记作，，该差值也表现为量子化特征，能级和能级差均随着量子数n的增大而增大。。

（3）关于本征波函数 

图1.3-2描述了边长为的一维势箱中粒子的波函数和概率密度分布。

由图可见， 和均是坐标x的函数，粒子在区间0<x<中不同位置上出现的概率密度是不同的。为正弦函数，波函数可为正值也可为负值，体现粒子的波动性。根据波函数的连续性，波函数由正变负，必然经过=0的点。通常除了边界点（对于一维势箱为x=0，x=处）外的波函数为零的点被称为节点。对于一维势箱的不同状态，其节点数为n-1个。

            

说明一维势箱中运动的粒子能量越高，波长越短，物质波的波长也是量子化的。

        

二、线性谐振子

分子中的原子均在各自的平均位置上作永不停息的振动。双原子分子的振动可看作是一个谐振子的振动。在宏观现象中,一个在平衡位置re 附近某处, 由于受到一个与位移r - re 成比例的恢复力f 的作用而往复振动的质点称为线性谐振子。f = - k(r - re)= - k x，式中比例常数k 称为弹力常数, k = 4π2 ν2 m ,m 是谐振子的质量,ν 是振动频率。x为位移,因恢复力与位移方向相反,故有一个负号。由于f = - d V/d x ,因此, 势能。
用量子力学处理线性谐振子,它的薛定谔方程为:

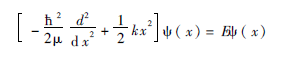
解此二阶常微分方程,得能量本征值为：

式中,υ 是振动量子数。

量子力学处理微观体系的一般步骤如下：

(1) 写出体现体系的特征势能算符，进一步写出体系的能量算符和能量方程。 

(2) 根据边界条件和归一化条件求解体系的能量方程，确定体系的能量和波函数。

(3) 绘制能级图和波函数及几率密度图，根据图形特点分析粒子的分布特点。

(4) 有了波函数，可以根据波函数求得该状态下各种物理量的本征值或平均值，预测和解释体系的性质。

(5) 联系具体的实际问题，将所获得的结果加以应用。