实践主题

从原子光谱出发研究原子结构。

实践目标

结合本章相关知识，与身边的同学进行讨论，对单电子原子定态薛定谔方程的解加以分析，以帮助同学们更好地掌握本章的学习内容。

实践任务

已知氢原子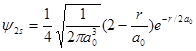 

实践要求

1.求节面半径

2.求几率密度极大半径

 

教师分析

任务1 ：

波函数为零的面即为节面（端点除外），因此求节面半径只需令将r解出即可。

令：

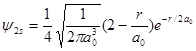 =0

解得r1=2a0, r2=（是端点，不合题意舍去）。所以波函数节面半径在r=2a0处。

任务2：

在教学上，若求函数f(x)的极值，须令df(x)/dx=0，解得Xi(i=1,2,……)，如果d2f(Xi)/dx2<0，则函数f(x)在Xi处有极大值f(Xi)；如果d2f(Xi)/dx2>0，则函数在Xi处有极小值f(Xi)。上述讨论应排除端点。

几率密度为

=

=

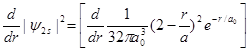
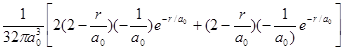
令

即：

解得：，不符合题意，舍去。

，因为我们已经求出为节面半径，此时几率密度为零，故为极小值，舍去。

即几率密度极大半径为r=4a0