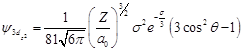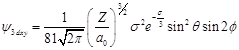单电子体系的直角坐标下的Schrödinger方程：

 

             （2.1-1）

由于在直角坐标下求解上方程过程比较复杂，所以一般把直角坐标转化为球极坐标。球极坐标如图2.1-1所示，两体系的坐标变量关系为：

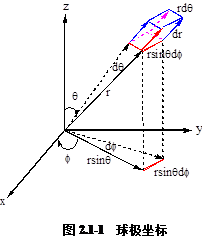
x = rcosqsinf   

y=rsinq sinf   

z=r cosq      

r2=x2+y2+z2

各变量的取值范围为：

r：0～∞，q：0～p，f：0～2p，dt = r2sinqdrdqdf

按照偏微分关系运算可得几个典型算符在球极坐标内的情况：

所以，球极坐标条件下的Schrödinger方程可写为:

 （2.1-2）

（2.1-3）

1.分离变数法

在球极坐标下，氢原子和类氢离子的Schrödinger方程（2.1-5）两边同乘以、并将含r项移到方程一边得：

+(E+)ψ=--（2.1-4）

由于算符中三个变量r、θ、φ分别独立存在于三部分，因此可用分离变量的方法进行分离，把方程(2.1-4)分成各含变量 r、θ、φ的三个方程：

，并用=乘以方程两边得：

 

令方程两边等于同一常数β得：

                      （2.1-5）                 

       （2.1-6）

将（2.1-6）两边乘以sin2θ并整理得：

sinθ×+βsin2θ+=0

令=并在方程两边同乘以得：

+βsin2θ=

令方程两边等于同一常数m2得：

+βsin2θ=m2     （2.1-7）

=-m2                    （2.1-8）

经变数分离得到的三个分别只含f，q和r变量的方程依次称为F方程、Q方程和R方程，解这三个常微分方程，求满足品优条件的解，再将它们乘在一起，便得Schrödinger方程的解。

2.方程的解

F方程（2.1-8）经过变数分离并整理得到：

     

为二阶常系数齐次线性方程，有两个复数形式的独立特解：

          

式中A可由归一化条件得出：

，

        (2.1-9)

应是f的单值函数，f变化一周，应保持不变，即，，eimf=eim(f+2p)= eimf

ei2mp，要求ei2mp=1。根据Euler公式：eif=cosf+isinf，则有cos2mp+isin2mp=1, m的取值必须为m=0，±1，±2，… 。m是量子化的称为磁量子数。

复数形式的F函数是角动量z轴分量算符的本征函数，但复数形式不便于用图形了解原子轨道或电子云的分布，需通过线性组合为实函数解。

先将(2.1-9)指数形式写成三角函数形式：

  

   

它们的任意线性组合仍然是F方程的解。在此我们作如下组合：

  

归一化的实函数解为：     

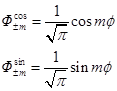        (2.1-10)

复函数解和实函数解是线性组合关系，现将m=0，±1，±2时的复函数解和实函数解列成下表：    

表2.1-1  Φ(f)方程的复函数和实函数解

M	复函数解	实函数解
0
1
-1
2
-2

对于方程可用级数法求解，但求解由于过程比较复杂，在此只给出方程解的结果：

（1）b＝，=0，1，2，3，…，称为角量子数。

（2）m＝0，±1，±2，±3，…，±，m称为磁量子数。

（3）方程由两个量子数、|m|确定。

对于方程将b＝代入后变为：
(2.1-11）

称为关联拉盖尔（Laguerre）方程，解此方程得到：

（1）当能量取负值，且

   n=1，2，3，… ，方程才有收敛的解。

（2）n≥+1, ＝0，1，2，3，…，n-1。

(3) 方程由量子数n、确定。

3.单电子原子的波函数

由上面Schrödinger方程的解，可得类H离子波函数为

  （2.1-12）

为单电子波函数，也称为原子轨道。其中称为波函数的径向部分；称为波函数的角度部分，是球谐函数。

F，Q，R，Y，y都归一化：

常用s，p，d，f，g，h，…依次代表=0，1，2，3，4，5，…的状态，原子轨道的名称与波函数的角度部分直接相关，例如，即称为1s 轨道；，即称为2pz轨道。氢原子和类氢离子的单电子原子波函数见表2.1-2。

表2.1-2  氢原子和类氢离子波函数

n	l	m	ψ
1	0	0
2	0	0
2	1	0
2	1	±1
3	0	0
3	1	0
3	1	±1
3	2	0
3	2	±1
3	2	±2

()