1.量子数的物理意义

（1）主量子数n

(i). 确定能量  对单电子原子而言，主量子数n决定体系能量的高低

(eV)           (2.2-1)   

n的取值为1，2，3……，当n无穷大时，体系的能量趋近于0，这样的物理模型可以被当做参考体系的零点。
能级差随主量子数n的变化关系：

所以，随着主量子数n的增大，能级差是逐渐减小的。

(ii)确定简并度  具有相同能量的不同状态的个数称为简并度。

对于单电子体系，只要n值相同，就具有相同的能量，但可有不同的l和m值，它们代表着不同的状态，这些状态互称为简并态。简并度与量子数的关系可表示为：

(iii)确定波函数的节面个数  波函数等于零的点所构成的平面或曲面称为节面。

径节面数 = n- l -1；角节面数 = l；总节面数 = 径节面数＋角节面数 = n-1。

(2)角量子数

将角动量平方算符作用于上可得下式：

                      

的本征值和角动量大小分别为

            （2.2-2）

可见，l决定电子的轨道角动量的大小，因此，称其为角量子数。另外，原子的角动量和其磁矩()有关，其关系为：

   （2.2-3）

其中为Bohr磁子，。

(3)磁量子数m

在解F方程时引入了磁量子数m，物理意义是：决定电子轨道角动量在磁场方向上的分量Mz，也决定轨道磁矩在磁场方向上的分量。

将角动量在z轴上的分量算符作用于上可得如下式：

                    

所以

                  （2.2-4）

同样，轨道磁矩可以求出，得到

角动量在磁场方向分量的量子化，已通过Zeeman效应得到证实。

(4)自旋量子数s

电子除了有轨道运动外，还有自旋运动，自旋量子数为s=，自旋磁量子数为。

自旋运动角动量的大小为：

                             （2.2-5）

自旋运动角动量在z轴的投影：

                                  （2.2-6）

同时伴随自旋运动又有自旋磁矩，其大小

它在z轴的分量为：

其中，ge为电子的自旋因子，，由于电子磁矩方向与角动量方向相反，故加负号。

(5)总角量子数j

因为电子的轨道运动与自旋运动的角动量都是矢量，电子的总角动量Mj就是两者的矢量和，Mj= M + Ms，它的大小由总角动量量子数j决定。若轨道角动量量子数为l，自旋量子数为s，则总角动量量子数

         （2.2-7）

（2.2-7）适合于任意两个角动量的耦合。总角动量的平方为

                （2.2-8）

角动量大小为

                                        

对于任何一个角量子数为L的角动量，这个角动量的平方值总是

            （2.2-9）

其大小为

          （2.2-10）

反过来，知道了角动量大小，可推出角量子数。

(6)总磁量子数mj

对于任何一个角量子数为L的角动量，其沿某坐标轴的投影（若存在磁场就是磁场方向，通常取作z轴）为

电子的总角动量Mj沿z轴的分量Mjz为

因为轨道角量子数l是整数，s=1/2，所以对于单电子体系j是半整数。

这样，描述单电子原子状态的量子数有上述6个，但其独立的量子数只有4个，可采用量子数（n,,m,ms）或（n,,j,mj）来描述。

2 波函数和力学量

Ψnlm(r,θ,f）描述单电子原子的运动状态，还是能量算符、角动量平方算符、角动量在z轴方向的分量共同的本征函数：

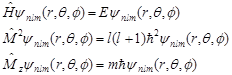
若单电子原子处ψnlm(r,θ,f）描述的本征态中，由以上本征方程可以求出力学量的本征值：

，，

但对于非本征态，如氢原子核外电子处于轨道时，对应的波函数是实函数由与组合而成，也就是由这两个态叠加而得，即，不是算符的本征函数，因此没有确定的值，只有平均值:。

对任意力学量，在波函数Ψnlm(r,θ,f）描述的状态下，其平均值（期望值）

3 电子云的图形表示

(1)y-r 和y2-r图

的分布具有球对称性,核外等距离r处的球面上各点的y值相同，几率密度y2的数值也相同。

H原子（Z=1）的1s和2s态波函数采用原子单位可简化为：

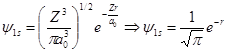
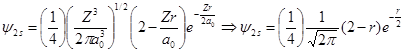
对于1s态：核附近电子出现的几率密度最大，随r增大稳定地下降。

对于2s态：在r<2a0时，分布情况与1s态相似；在r=2a0时，y=0，出现一球形节面（节面数=n-1）；在r>2a0时，y为负值，到r=4a0时，负值绝对值达最大；r>4a0后，y渐近于0。

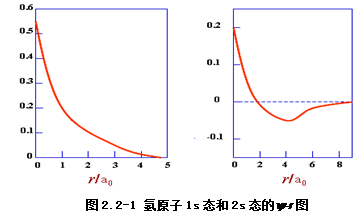
1s态无节面；2s态有一个节面，电子出现在节面内的几率为5.4%，节面外为94.6%；3s态有两个节面，第一节面内电子出现几率为1.5%，两节面间占9.5%，第二节面外占89.0%。

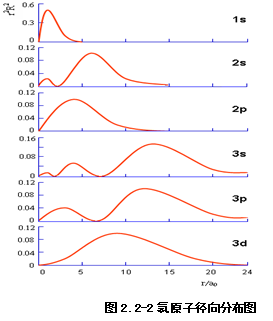
(2)径向分布图

其物理意义：Ddr表示在半径r→r+dr两球壳层内找到电子出现的几率，它反映了电子云的分布随半径r的变化情况。将dt在q和f的全部区域积分，即表示离核为r，厚度为dr的球壳内电子出现的概率。

图2.2-2为H原子的径向分布图。在径向分布图中，除原点外，的面为径向节面。

由图2.2-2可以看出：

（1）每一个n和确定的状态，有n－个极大值和n－－1个径向节面。

（2）n相同时：越大，主峰离核越近；越小，峰数越多，最内层的峰离核越近；相同时：n越大，主峰离核越远；说明n小的轨道靠内层，能量低。

(3)角度分布

从坐标原点引方向为、长度为的射线，所有这些射线的端点在空间所组成的曲面，称为原子轨道的角度分布图。由Y=0产生的节面称为角节面。

=0°对应于z轴的正方向，=180°对应于z轴的负方向。

按cos计算出不同值时的Y值，因为只含而不含有，图2.2-3给出不同原子轨道的角度分布图。

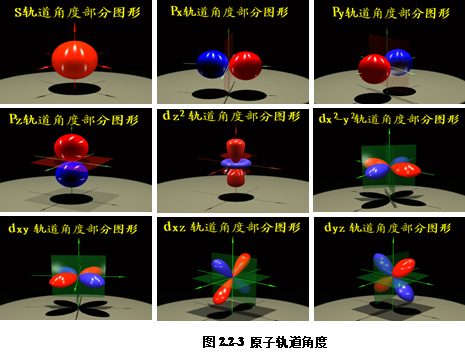
(4)空间分布

空间分布图有多种表达形式，如电子云图、原子轨道轮廓图、等值线图以及界面图、网格立体图等。下面只简单介绍电子云图和原子轨道轮廓图。

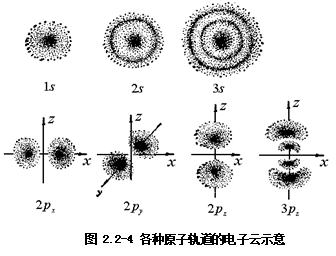
(i)电子云图。  将的大小用小黑点在空间分布的疏密程度来表示的图形称为电子云图，见图2.2-4。

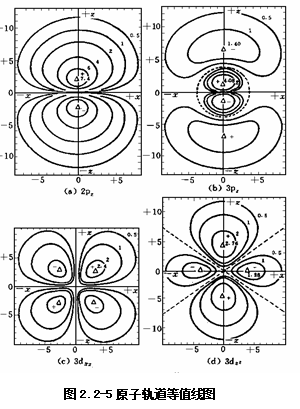
(ii)原子轨道等值线图  y(原子轨道)随r，q，f改变，不易画出三维图，通常可画截面图，把面上各点的r，q，f值代入y中，根据y值的正负和大小画出等值线，即为原子轨道等值线图。

(iii)原子轨道轮廓图。 

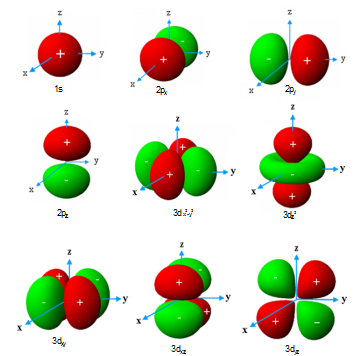
图2.2-6 原子轨道轮廓图（各类轨道标度不同）

把y的大小轮廓和正负在直角坐标系中表达出来，以反映原子轨道空间分布的立体图形叫做原子轨道轮廓图，或简称原子轨道图，如图2.2-6所示。原子轨道图为了解成键时轨道重叠情况提供了明显的图像。