1.多电子原子的Schrödinger方程

对于原子序数为Z，含n个电子的原子，其Schrödinger方程为：

()＝En                      （2.3-1）

这里由于的存在，使得无法将各个电子相互分离，而忽略电子之间的相互作用引起的误差又是很大的。这时，可以把多电子原子中的每个电子看作是在原子核和其余n-1个电子共同形成的平均势场中运动，用单电子函数来描述其运动状态，称为单电子近似。这种用来描述原子中单个电子运动状态的波函数称为原子轨道，单电子的Schrödinger方程为：

式中yi是所考虑电子的坐标函数，V是该电子与其余n-1个电子之间的排斥能。V除了和所考虑的电子坐标有关，还和其余n-1个电子的坐标有关。作为一种平均情况，可以认为第i个电子是在其余n-1个电子所形成的电子云的云雾中运动，势能V与其它n-1个电子的运动状态有关，当其余n-1个电子状态一定时，V就只是所考虑的电子的坐标的函数了。但这时V仍然是电子i的三个坐标r、q、f的函数，不能进一步分离变量，方程仍然难以求解。

2.中心势场近似

将原子中其他n-1个电子对所考虑电子i的排斥作用看成是球形对称的、只与径向有关的力场，称为中心势场近似。在中心势场近似的情况下，第i个电子受其余电子的排斥作用看成相当于si个电子在原子中心与之相互排斥。第i个电子的势能函数可写成：

    （2.3-2）

此式在形式上和单电子原子的势能函数相似，Z*称为有效核电荷。

因此，中心力场模型下多电子原子中第i个电子在原子单位下的Schrödinger方程为：

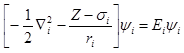  （2.3-3）

此方程中的坐标ri不再是位置矢量，而只代表径向坐标，不再涉及角向坐标。方程中描述原子中单电子运动的空间波函数为原子轨道。

3.原子轨道能量计算

在单电子近似和中心力场近似的基础上，解多电子原子的Schrödinger方程还需要知道电子间的势能V，考虑到用变分法处理氦原子的结果，每个电子与另一电子的相互作用可以看作起到了核电荷屏蔽的作用，表现为好像是抵消掉了部分核电荷，若用表示第i个电子对第j个电子的核电荷屏蔽，那么对第j个电子总的屏蔽系数为：

                                          

原子核对第j个电子有效核电荷为：，则电子所处的轨道能量Ei 公式为：

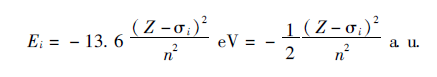
角量子数为1, 2, 3, ...的s, p, d...电子对同一电子的屏蔽作用各不相同，多电子原子体系的轨道能Ei 由主量子数和角量子数共同确定。对单电子原子来说，ns和np是简并的,但对多电子原子来说这种简并解除了。