1.电子自旋的假设

原子光谱的精细结构发现，氢原子中电子1s®2p跃迁，高分辨率的光谱仪观察到两条靠得非常近的谱线。Na光谱的黄线（价电子3p®3s）也分解为波长差为0.6nm的谱线。1921年，斯特恩(Stern)和盖拉赫(Gerlach)在实验中发现碱金属原子束经过一个不均匀磁场射到一个屏蔽上，发现射线束分裂为两束向不同方向偏转。

1925年，荷兰物理学家乌仑贝克和哥西密特提出电子具有不依赖于轨道运动的固有磁矩的假说。这就是说，即使处于s态的电子，l=0，，轨道角动量为0，但仍有内在的固有磁矩。如果我们把这个固有磁矩看成是电子固有的角动量形成的，这个固有的角动量形象地用“自旋”来描述。电子的自旋并不是电子顺时针或逆时针方向旋转，而是电子具有非空间轨道运动的角动量。

每个电子都有自旋角动量，它在空间任何方向的投影都只能取两个，自旋磁矩与轨道运动产生的磁矩会发生相互作用，常称为轨旋耦合。由实验知道，电子的自旋角动量在磁场方向的分量只有两个分量，所以ms的取值只有两个。单个电子自旋量子数s=1/2，自旋磁量子数ms=±1/2。

电子的自旋轨道常用希腊字母a和b表示，分别对应ms=1/2和ms=-1/2，同时也是自旋角动量平方算符的本征函数。

自旋运动波函数满足正交归一性

            

即

上面式子中，m为自旋坐标，只有2个值。若考虑电子的自旋，一个电子运动状态用波函数来描述。

                 （2.4-2）

自旋角动量平方算符作用到自旋函数上，有

                             （2.4-3）

自旋投影算符作用到自旋函数上，得

                                  （2.4-4）

  

2.行列式波函数和保里(W.Pauli)原理

电子是全同粒子，即电子是不可区分的。

保里(Pauli)原理¾¾对具有半奇整数自旋量子数的粒子（例如电子），所有合适的波函数必须对任何两个全同粒子的坐标变换是反对称的。

即            (2.4-5)

波函数的坐标包括每个电子的空间坐标和自旋坐标。

为满足全同粒子和保里原理，描述一个电子的完全运动状态应该用行列式波函数来描述。

以He原子为例(1s2)，有两种可能的运动状态：

                   

二者均不符合反对称的要求，但它们的线性组合

 

是符合Pauli原理的，归一化，书写成行列式形式：

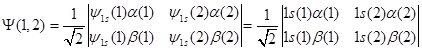  (2.4-6)

对于n电子体系基态，行列式波函数为

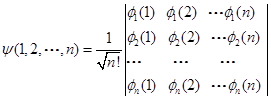        (2.4-7)

在上面的行列式中，每一行中所有函数都相同而每一列中坐标都相同。交换两列相当于交换两个电子的坐标，行列式的值符号改变，满足交换的反对称性。若行列式中两行元素相同，即n, l, m, ms均相同，此时行列式的值为零。由此得出保里原理的推论：两个电子不能具有四个相同的量子数（n, l, m, s），自旋相同的两个电子之间存在保里斥力。这实际上，就是在一个相同的空间轨道上，最多能容纳两个自旋相反的电子

3.原子核外电子排布

基态原子核外电子排布遵循以下三个原则：

（1）保利原理

原子中不能有两个或更多个电子具有完全相同的4个量子数n，，m，ms，也就是说，每一个量子态只能容纳一个电子，对于给定的n和，考虑自旋，共有2（2+1）个量子态。因此根据保利原理最多只能容纳2（2+1）个电子。对于一定的n，s态最多只能容纳2个电子（这两个电子自旋方向相反），p态为6个，d态为10个，f态为14个。

根据Pauli原理，原子内具有相同主量子数n的量子态，只能容纳2n2个电子。n=1最多只能容纳2个电子，n=2为8个，n=3为18个，n=4为32个。

（2）能量最低原理

电子的排布，在不违背保利原理的条件下，基态电子优先占据能量较低的原子轨道，使整个原子体系总能量处于最低。由于影响原子轨道能量有诸多因素，情况比较复杂，为此，我国科学家徐光宪教授从大量光谱数据归纳出经验规律：在绝大多数情况下，核外电子按n+0.7的次序排列在各原子轨道上。

（3）洪特规则

在主量子数n和角量子数相同的轨道（能级简并的轨道）上排布的电子将尽可能占据不同的轨道，且自旋平行；全充满、半充满、全空的状态比较稳定，因为这时电子云分布近于球形。以碳原子1s22s22p2为例，如2个p电子在同一轨道上排斥力大，而在不同轨道且自旋平行时排斥力小，电子按洪特规则，即以上第二种方式分布可使体系能量最低，最稳定。