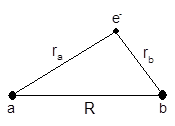
H2+的模型

在波恩- 奥本海默(Born -Oppenheimer)定核近似下, H2+ 体系中电子运动的薛定谔方程为:

    

上式中的E是含电子能量和核排斥能在内的H2+分子体系的能量,而波函数则描述了在该确定核构型下电子的可能运动状态。

1.变分原理和线性变分法

求解上述方程需要利用变分原理。变分原理的定义是：若为给定体系的哈密顿算符，f 为满足体系边界条件的品优函数，则下式成立：           

             

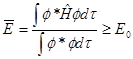
此式称为变分积分。式中f 称为变分函数, E0为体系基态能量，表明体系关于f 的平均值E存在极小值，这就是变分原理。

当运用变分原理过程中，如果变分函数是采用一组满足体系边界条件且线性无关的品优函数）的线性组合来构造，则被称为线性变分法。即线性变分函数为：

    

是函数的线性组合系数。

把变分函数代入变分原理式可得：

        

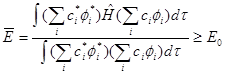
积分后变分积分只剩下为待定常数。即:

                       

在极小值点有:

         

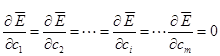
由此可得m 个求解的联立方程组，称为久期方程。运用线性代数方法可求得久期方程的m套非零解。其中与最低值对应的一套解，组成电子基态近似波函数，该便是相应基态能量的近似值。

2.分子轨道（MO）和原子轨道线性组合成分子轨（LCAO-MO）

如果由a氢原子和b氢原子的原子轨道和 的线性组合来构造H2+的变分波函数，则

                     （4-1.7）

描述的是分子中单电子的运动状态，称为分子轨道，并把由原子轨道线性组合为分子轨道法简写为LCAO-MO法。

3.久期方程组、久期行列式及其解

     （4-1.8）

这是待定系数c1 、c2的齐次线性方程组，其中

           （4-1.9a）

                       (4-1.9b)

                   (4-1.9c)

                            (4-1.9d)

数学上，必有c1= c2=0的一组解，但这组解会导致波函数为零 ，与H2+有一电子的物理事实相悖；这就需要去求c1 和c2的非零解。

根据数学相关知识，c1 和c2的非零解的前提条件是下式必须成立:

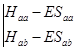
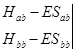    =0                 (4-1.10)

该式被称为久期行列式。

展开行列式得：

   (4-1.14)

E有两个解:

                              

                              （4-1.15）

若、为H的1s轨道，E1、E2即为H2+ 的基态和第一激发态的能量解。

（d）久期方程的解  把E1代入4-1.12式，可得c1= c2=c'，相应的波函数为:

                       （4-4.16）

利用归一化条件有：

      

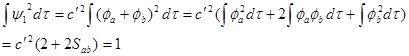
即归一化常数:                   

把E2代入4-1.12式，用同样的方法可求得。

这样，H2+基态和第一激发态分子轨道波函数为:

      

                  (4-1.17)

4.解的讨论   

(a）和 

 称为重叠积分（常简写为S），代表了、在分子中重叠程度。

R→∞, Sab=0         R=2a0, Sab=0.586         R=0, Sab=1

(a)              (b)              (c)

图4-1.2  φa..1s和φb.1s间的重叠

 

称为库仑积分（常写为α）：

   

                             (4-1.18)

在平衡核间距处J约为的5%。故。

称为交换积分（常写为β）：

（4-1.19）

 

在平衡核间距处，K<0、>0、，故 。               

(b) E1和E2   

 

                              

 

因E1、E2都是核间距R的函数，能量随R 变化的曲线如图4-1.3。E1—R曲线有能量最低点，此处的R值称为平衡核间距记为Re，对应的能量为H2+的离解能De。该曲线还表明，当H 和H+从无穷远处相互接近时，体系能量逐渐降低，直到R=Re时形成稳定分子。故称与E1对应的态为吸引态、成键态是H2+的基态。而曲线Ⅱ没有极小值，E2随R的增加而单调下降，直到时。即E2对应的状态始终比原子体系的能量高，此状态下的H2+将自发地离解为原子体系，故被称为排斥态、反键态，是H2+的第一激发态。

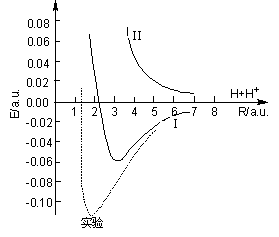
图4-1.3  H2+的能量曲线

(以H+H+体系能量为原点, I 和 II分别为能量E1、E2对R的曲线)

为了简明地表示能量的相对关系，在忽略后，H2+的能量为:

               （4-1.20a）

                (4-1.20b)

H2+的MO能级图

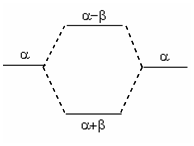
图4-1.4  H2+的MO能级图

（c） 

      

是H2+的吸引态、成键态，当电子排入该轨道时可使分子体系能量降低，称为成键分子轨道。而描述的是排斥态、反键态，当电子排入其中可使分子能量升高，称为反键分子轨道。

图4-1.5给出了、的等值线图。在二核之间有较大几率振幅，没有节面，而在核间值则较小且存在节面。从该图还可以看出，分子轨道不是原子轨道电子云的简单的加和，而是发生了波的叠加和强烈的干涉作用。

 

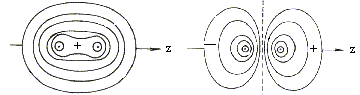
(a)            (b)

图4-1.5    H2+ 的(a)和(b)的等值线图

（d）共价键本质  

H2+成键态电子云图表明，成键后电子云向两核间集中，被形象地称为电子桥。当二个原子相互接近时，由于原子轨道间的叠加，产生强烈的干涉作用，使核间电子密度增大，核间大的电子密度把两核结合到一起，使体系能量降低，形成稳定分子，带来共价键效应。