1.分子中的单电子波函数—MO

在定核近似下，若分子体系含有m个核及n个电子，哈密顿算符为：

   （4-1.21）

与多电子原子的情况一样，最常用的解决办法采用单电子近似（轨道近似）。分子体系中单电子有效哈密顿算符可写成：

               （4-1.22）

式中 ，此时分子体系的单电子薛定谔方程式为：

                      （4-1.23）

式中单电子波函数yi为分子轨道波函数，相应的本征值Ei为分子轨道能。

对于给定分子的任何一个MO都可以由有关的AO线性组合而成，即:

                    （4-1.24）

称为yj的基函数。

 

2.满足有效组合成分子轨道的原子轨道的条件——LCAO —MO三原则

以双原子分子AB为例。

若为A原子的轨道，为B原子的轨道，它们的能量和类型均不同。将两者线性组合:

                  （4-1.25）

根据前一个知识点和 的定义，，，此处和取为轨道和的能量。

应用变分法处理，并略去项，所得到的久期方程是:

              （4-1.26）

解相应的久期方程:

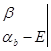  = 0               （4-1.27）

能量为（此时假定）:

  

设        （4-1.28）

则   ，             （4-1.29）    

因，h应为正值，可做出能级图4-1.6。

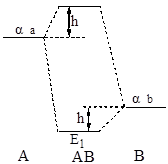
 图4-1.6 分子AB的MO能级示意图

当电子排入E1能级以形成双电子键时，则分子AB的离解能可表示为:

   （4-1.30）

显然, 成键效果决定于（）和的数值。再将和分别代入相应的久期方程（4-1.26）式:

         （4-1.31a）

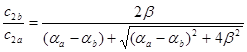        （4-1.31b）

与和相对应的两个分子轨道为:

                          （4-1.32a）

                         （4-1.32b）        

从4-1.28， 4-1.29, 以及4-1.31式可见，若则h=0, 两个原子轨道、不能有效地组合成分子轨道。

那麽、间要满足什么条件时？

• 对称性匹配原则  

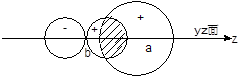
      以、轨道组合成分子轨道(图4-1.7a)以及而轨道组合成分子轨道(图4-1.7b)时的情况为例。

 

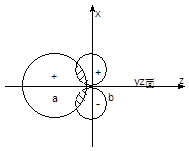
（a）               (b)

图4-1.7  LCAO-MO对称性匹配的条件

显然图4-1.7b可以组合成分子轨道，这就是LCAO —MO中的对称性匹配原则。

(b) 最大重叠原则 

现在讨论在时，使LCAO—MO产生最佳效果的条件。

从4-1.28和4-1.29式可知，在和确定的条件下，值越大，意味着两个轨道组合效果越好；而根据上一个知识点中的-1.19式可知

交换积分β

 

即要求应尽可能的大，这就是最大重叠原则。

如何能使、间产生最大重叠呢？这除了与两原子核间距离有关外，还将与接近的方向有关。

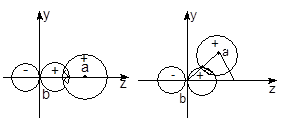
图4-1.8给出了在相同核间距时和=沿不同方向重叠的情况。该图表明，当沿的极值方向重叠时方可有最大重叠效果，这决定了共价键具有方向性。

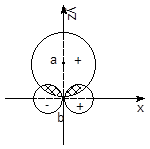
(a)        (b)          (c)       

图4-1.8 φs和φpz沿不同方向重叠对Sab的影响

[ Sab（a）＞ Sab（b）＞ Sab（c）= 0 ]

(c) 能量相近原则 

进一步讨论和的取值对、组合效果的影响。

因为      

表明，当>>即和间能量差很大时，将有->>2，h0。

此时E1、E2，说明线性组合后的MO能量还原为AO能量，即ψ1、ψ2。而当=时，可得h=、C1a= C1b和C1a= -C1b，能有效组合成分子轨道，类似于H2+中的结果。