价键理论从经典化学键模型出发，把研究的对象集中在直接键联的两个原子上。海特勒（Heitler）和伦敦(London)在讨论氢分子的结构时提出一种双电子键波函数，把它带入H2 的薛定谔方程用变分法解获得成功，开创了价键理论的先河。在此基础上，泡林（Pauling）提出杂化轨道理论，使价键理论逐渐完善。

1.价键法对氢分子的求解

定核近似下氢分子的薛定谔方程：

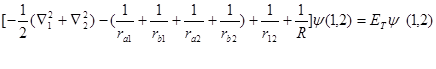
（4-4.1）

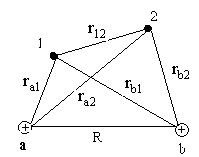
图4-4.1  氢分子模型

当氢原子a和b相互接近时，通过交换或共享这对电子而成键，假设电子1在a核附近而电子2在b核附近时的运动状态分别可用a、b两原子的AO来描述，此时双电子的状态可用下面的波函数来描述：

                    （4-4.2）

而当电子2运动到a核附近而电子1到b核附近时，双电子的状态为：

                    （4-4.3）    

海特勒和伦敦运用这两个波函数进行线性组合来描述氢原子键合成分子后的电子状态，该试探波函数被称为双电子键波函数。

           （4-4.4）

将其带入变分原理表达式，并利用变分法求解（过程与H2+同），可得双电子键波函数的解为：

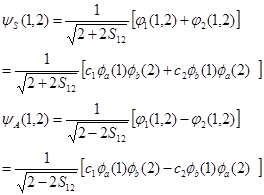    （4-4.5）

而分子的能量解为：

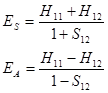                           （4-4.6）

式中：

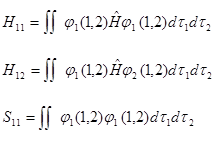               （4-4.7）

由于H11、H12和S11积分后仅是核间距R的函数，可做ES、EA对R的曲线图。

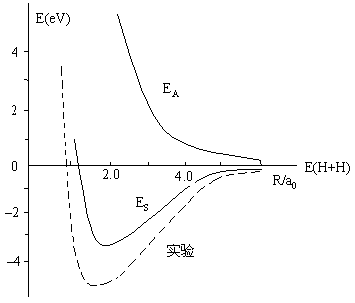
图4-4.2   海特勒-伦敦法解得的H2分子能量曲线

由图4-4.2 可知， 态为成键态，态是反键态。由海特勒-伦敦法解氢原子得的平衡核间距Re 等于87pm,、离解能De 等于3.14eV, 而实验值分别为74.2pm 和4.72eV。该结果说明海特勒–伦敦法讨论氢分子结构是成功的。

2.双电子完全波函数

前面的章节已提及电子除了作空间运动外还有自旋运动，完整的电子运动状态的描述除了有空间波函数外还应含自旋波函数。

若用空间波函数与自旋波函数的乘积波函数作为分子的完整波函数，则根据保利原理，交换电子1、2的坐标分子的完整波函数应呈反对称。

由4-4.5 式可知，交换电子1、2 的坐标，双电子空间波函数呈对称、双电子空间波函数呈反对称，因此还须构造对称与反对称的双电子自旋波函数。

最简单的双电子自旋波函数有以下四种：

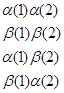                    （4-4.8）

前两个呈交换对称性，后两个呈交换非对称性，但可以将非对称性的双电子自旋波函数进一步线性组合，形成如下的组合形式，其中一个是交换对称的双电子自旋波函数，另一个是交换反对称的双电子自旋波函数：

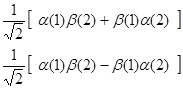        （4-4.9）

这样，由海特勒-伦敦法解得的H2分子的完整的成键波函数是：

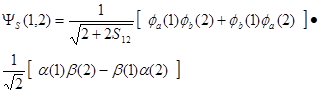（4-4.10）

由于H2分子的成键态对应只有一种自旋态，所以是单线态。

而完整的反键波函数应是：

 

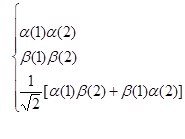               (4-4.11)

所以H2分子的反键态是自旋叁重态。

该结果给了我们这样一个图像：当两个氢原子相互接近成键时，若两电子自旋反平行可配对成键；而若两电子自旋平行，则成排斥态，不能形成稳定分子。所以，价键理论又被称为电子配对理论。

3.价键理论与分子轨道理论对比

分子轨道理论以单电子在整个分子范围内的可能运动状态—分子轨道为基础讨论分子的电子结构，价键理论则以分子中直接键联原子间的双电子键波函数为基础讨论分子的电子结构。因此，价键理论和分子轨道理论在研究分子中的电子状态时分别具有“定域”和“离域”的特征。

两者的区别较为明显。以氢分子基态为例，MO法得到的双电子波函数为：

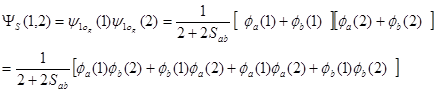
（4-4.12）

与4-4.5 式相比，4-4.12 式中明显多了后面两项，而这两项描述了两个电子出现在同一原子轨道的情况，或分子的离子状态（H+H—）。前两项描述的氢分子化学键中的共价键成分与后两项描述的的离子键成分是等同的，显然夸大了离子键的贡献；而4-4.5 式说明价键理论的海特勒-伦敦法完全忽略离子键成分的贡献也是不完善的。

目前，发展中的分子轨道法和价键法不断改进、优化基函数的选取和组合方式，计算结果越来越精确、相互也越来越接近。另一方面，分子轨道法吸纳了出自价键法的杂化轨道理论去讨论分子的几何结构，丰富了MO法；价键理论也吸纳、借鉴分子轨道理论的优点，不断完善，使得现代价键理论迅猛发展。