一、双原子分子光谱

分子光谱是把分子发射出来的光或被分子所吸收的光进行分光得到的光谱。分子光谱与分子内电子和核的运动密切相关，光谱中每根谱线是分子在二个能级间跃迁的结果，是测定和鉴别分子结构的重要实验手段，也是分子轨道理论的实验基础，主要包括紫外可见光谱和红外光谱。

1.双原子分子整体运动的分解及相应光谱

分子内的电子和核运动可以进行分离，通过解电子运动方程，得到了电子能量Ee。当把核的相对运动分解成振动(能量记为Eｖ)和转动(能量记为Er)时，分子的总能量应为:

EＴ＝Ee＋Eｖ＋Er                       (4-5.1)

当分子的运动状态变化时，总能量的变化可写成:

△ＥＴ＝△Ee＋△Eｖ＋△Er                (4-5.2)

对应光谱所在波段如表4-5.1所示。

表4-5.1   转动、振动和电子光谱所在的波段

由上可知，电子运动状态的改变引起能量的变化幅度最大，必将引起振动和转动状态的改变，将产生电子-振动-转动兼有的复杂谱带。振动状态的改变将产生振动-转动兼有的光谱，而转动光谱相对简单。

2.双原子分子的转动光谱

(1)刚性转子模型近似 若把原子A和B视为质量为ｍＡ和ｍB的质点，分子在转动过程中原子间距离不变，为平衡核间距Re(如图4-4.1所示)，此时双原子分子的转动被近似看作为一刚性转子。

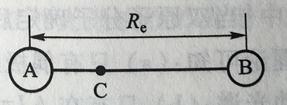
 图4-4.1 双原子分子AB的刚性转子模型

根据经典力学对刚性转子的讨论，转动能应为：

                             (4-5.3)

式中w 为转动的角速度,为转动惯量，其中m 为分子的约化质量。

对于双原子分子：

                          (4-5.4)

若C为质心，则刚性转子的运动等价于质量为m 的粒子作以Re为半径的绕质心的运动。这样角动量就是刚性转子的特征力学量。

                             (4-5.5)

故有：

                   (4-5.6)

考虑到刚性转子只有动能，由力学量算符化规则可得刚性转子的哈密顿算符：

                             (4-5.7)

相应的薛定格方程为:

                         (4-5.8)

上式可改写成刚性转子角动量平方算符的本征方程:

                            (4-5.9)

根据氢原子解已知，角动量平方算符的本征值是量子化的，为:

        ＝0，1，2……      (4-5.10)

可推得刚性转子能量也是量子化的，为:

    ＝0，1，2……       (4-5.11)

称为转动量子数。

  在光谱的研究中体系的能量(即能级)常用相应光子的波数来描述，被称为谱项。

转动谱项为:

    (4-5.12)

B称为转动常数，单位为ｍ-1。 当双原子分子确定后，B也就确定了。

转动光谱的选律：

(a)只有偶级矩不为零的分子才可能在电磁幅射作用下发生转动能级的跃迁，产生转动光谱；

(b)只有在△Ｊ＝±1或相邻能级间的跃迁几率(决定谱线强度)才是显著的。

(2) 转动光谱的应用

以HCl分子为例，当△J＝±1时各谱线的波数应满足

            (4-5.13)

式中 J 应为低转动能级的量子数。相邻谱线间的波数差

                          (4-5.14)

由于转动能级相差很小，室温下按Boltzmann定律分布在各能级上的分子数近，由此可推断，按照刚性转子模型描述的双原子分子的转动光谱应由一系列间隔相等的谱线(单位为ｍ-1)。  

3.双原子分子的振动光谱

(1)谐振子模型

双原子分子的振动是指两核的相对伸缩运动。当双原子分子电子组态确定后，分子能量随核间距变化的曲线如图4-4.3所示。图中也给出了谐振子的能量曲线。比较后可知在R＝Re处附近二能量曲线相当一致。因此用谐振子模型来讨论双原子分子的振动。

按照量子力学对谐振子的讨论，可把分子因核振动而偏离Re时所受的力写为:

                           (4-4.16)

被称为化学键的力常数，它的大小反映了化学键的强弱；此时核的振动能是量子化的 。

特征    u＝0，1，2，……       ( 4-4.17)

u称为振动量子数。特征频率的表示式为

特征                          (4-4.18)

式中m 为双原子分子的约化质量。

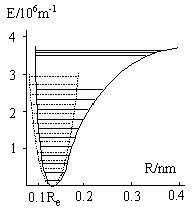
图4-4.3 HCl分子的势能曲线(实线为实测值，虚线为相应谐振子曲线)

由4-4.17式可知，即使在绝对零度下分子的振动能也不为零，而是

特征

称为分子的零点振动能。该结果为物质的运动是永恒的这一哲学命题提供了依据，也是量子力学不确定原理的必然结果。

(2)HCl的振动—转动光谱 在讨论分子的振动光谱时，常把振动能级用相应光子的波数来描述，称为振动谱项。

称为特征波数，单位为ｍ-1。

由量子力学含时间的微扰理论可知：(ａ)只有偶极矩随核间距 R的变化而变化的分子才有可能在外界电磁幅射作用下发生振动能级的跃迁，产生振动光谱。故同核双原子分子在通常情况下没有振动光谱。(ｂ)对于极性分子，只有△u＝±1能级间的跃迁是允许的。这两个条件为振动光谱的选律。

由此可得极性分子在相邻振动能级间跃迁产生光谱的波数为：

                      (4-4.20)

即满足选律的双原子分子振动光谱只有一条谱线，若以秒-1和米-1为单位时分别为n特征和。

分子的特征波数一般在400～800×102 m-1之间，在红外区，故分子的振动光谱称红外光谱。分子的转动常数B一般在1～400×102ｍ-1的远红外和微波区，故分子的转动光谱又称远红外光谱。分子在振动能级间发生跃迁时必将引起转动能级的跃迁。所以分子的红外光谱不仅含有核振动状态的信息也含有转动状态的信息，又被称为分子的振动—转动光谱。

4.双原子分子的电子光谱

当分子中电子在不同能级间跃迁时，可产生电子的吸收和发射光谱。与原子光谱相似,分子中电子的能级状态可用电子谱项来描述。

(1)电子谱项在原子中束缚电子运动的核势场是球对称的、单中心的，而双原子分子中束缚电子运动的核势场是椭球对称的、双中心的。故当取分子键轴方向为磁场方向时，分子轨道的角动量在磁场上的分量 Mz 成为描述电子运动状态的特征物理量。量子力学可以证明，此时Ｍz的取值是量子化的。

               m＝０，±1，±2，……    (4-4.24)令l＝｜ｍ｜，l 的取值与MO的类型间存在如下关系：

l ＝｜ｍ｜       0       1       2       3       ……

MO类型        sp  df     …… 

MO简并度        1       2       2       2       ……



对有ｎ个电子的双原子分子，其总轨道角动量在磁场上分量量子数为各占据轨道磁量子数ｍ之和。即:

                           (4-4.25)

与原子的谱项相仿, 不同的电子状态用大字的希腊字母表示。

       0       1       2       3       ……

状态    S            P              D             F              ……

这样电子谱项记为2S+1。此处S为电子的总自旋量子数。

对于S 态，还需在其右上角标明电子总波函数对过键轴平面的对称性。在大多数情况下为S＋状态，若有两电子自旋平行地占据p 或d 轨道时为S-状态。

由于同核双原子分子具有对称中心，电子总波函数对该对称中心呈对称或反对称，需分别用ｇ或ｕ标于电子谱项的右下角。总波函数的对称性由电子占据的MO对称性乘积来决定，规则为：ｇ×ｇ＝ｕ×ｕ＝ｇ，ｕ×ｇ＝ｇ×ｕ＝ｕ。

(2)电子光谱 电子光谱的选律为：(ａ)△Ｓ＝0。但重元素的双原子分子除外。(ｂ)DL＝０，±1。 对于Σ态，Σ+和Σ+、Σ-和Σ-间跃迁允许，而Σ+与Σ-间跃迁禁阻。(ｃ)对于同核双原子分子，只有对于对称中心对称性相反的谱项间（即ｕ、ｇ态间）的跃迁才是允许的，对称性相同的谱项间跃迁是禁阻的。

如前所述，分子中电子的跃迁必将伴随着核的振动能级和转动能级的跃迁，并此时振动能级可在△u 为任意值下跃迁。故电子光谱呈现复杂带状光谱。

综上所述，双原子分子的电子光谱虽然复杂，但它提供了很多有关分子结构的信息。如对H2、Ｏ2等非极性分子，因它们在核的振动、转动能级间的跃迁是光谱选律所禁阻的，得不到相应的光谱。但电子光谱可得到有关核振动和转动状态的信息。另外，对分子的电子光谱的研究，也促进了分子轨道理论的发展。

二、双原子分子光谱应用

通过双原子分子的转动光谱，可以确定化学键键长和研究同位素效应等性质。      

例1：若1H35Cl的远红外光谱中四根相邻谱线的波数分别为2118、4238、6354 、8472ｍ-1，试求其化学键键长。 

解：这四根谱线间距离基本相等,平均值为2118m-1,得B=1059m-1 ,属远红外波段。

 



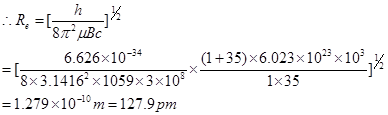
例2：试讨论1H35Cl和1H37Cl远红外光谱相同谱线间的。

解：1H35Cl和1H37Cl的化学键键长一样。当1H35Cl的某根红外谱线波数为:

1H37Cl相应谱线应为:

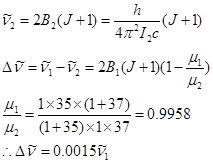
由上例可知B＝1059ｍ-1。取J＝0，有:



且 随J增大而增大。因自然界中存在37Cl，所以在HCl的高分辨远红外光谱或红外光谱中，每根主谱线旁有一较弱的伴生谱线。

下面举例说明双原子分子电子谱项的确定。

例3：H2+基态。

解：电子组态为1sg1 ，故＝０， , 电子谱项为。

例4：Ｏ2基态。

解：电子组态为1s1s 2s2s 3s1p1p。由于σ电子对Λ值的贡献为零，二重简并的1p u轨道(ｍ分别为+1和-1)上四个电子对L值贡献也为零，即闭壳层的贡献为零，只须考虑开壳层部分贡献。1p可有下面几种具体排布方式：

                

mi               +1   -1          +1  -1        +1   -1

L＝｜｜    0                0             2 

S＝｜｜    1                0             0 

电子谱项                             1

由洪特规则可知，是能量最低谱项。

例5：CO的基态和第一激发态。

解：基组态为：122232421p 452，是闭壳层，故为。

第一激发态组态开壳层部分为512p1，L＝１、Ｓ＝0、1。故电子谱项为     3Π和1Π。

例6：红外光谱测出 1H35Cl的 n特征＝8.667×1013ＨZ，求零点振动能和化学键力常数。

解：EV（u＝０）＝1/2ｈn特征

＝1/2×6.626×10-34×8.667×1013＝2.871×10-20J

ke＝4π2n特征m

＝4×3.1412×（8.667×1013）2×（1×３５）/[（１＋３５）×1/6.03×1023×1000]＝4.788×102Ｎ·ｍ-1            。

例7： 利用上题条件求 1H37Cl与 1H35Cl间特征波数之差△,这说明了什么?

解：∵=n特征/C

n特征＝                         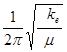

且同位素效应应不影响化学键的性质，可以认为二分子的相等。

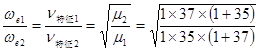∴=1.00075

∴△＝-＝(1-1.00075-1) ＝72.2ｍ-1

与在本节转动光谱例2中求得氯的同位素效应可使转动光谱谱线偏差3.2ｍ-1相比，说明同位素效应在振动光谱中反映更明显。