1.对称操作和对称元素

如果对分子图形进行某种操作后，不改变其中任何两点间距离，仍能得到分子的等价图形，并经过数次操作后使分子图形完全复原的操作称对称操作。例如图3.1中的BF3分子绕垂直于分子平面且经过B原子的直线(x轴)逆时针旋转120°后得到分子图形（2），（2）与未施加旋转操作时的图形（1）是等价的。如果（2）再旋转120°得到（3），（3）也与（1）等价。（3）再旋转120°又回到（1），分子图形完全复原。这个使分子旋转120°的动作就是对称操作。进行这个对称操作所凭借的直线(x轴)就叫做分子的对称元素。注意不要将对称操作和对称元素两个概念混淆，对称操作是一个动作，而对称元素是实施这个动作所凭借的几何要素（点、线和面）。

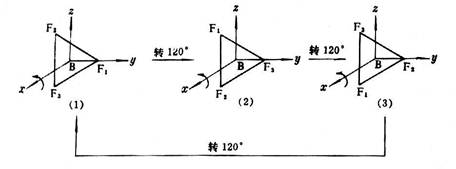
图4.1 BF3分子的旋转

2.分子的对称操作

一般说来，分子图形是有限图形，存在于分子中的对称操作有以下几种：

（1）旋转

借助一条直线使分子旋转 (n=1，2，3,……)后得到分子等价图形的操作称旋转，用表示；进行旋转凭借的直线称旋转轴或对称轴，记为。轴称作n次旋转轴，一个轴可产生n个旋转操作：，，，。表示绕该轴旋转，相当于分子不动

表示不对分子施加任何操作，称作恒等操作，是每个分子都有的对称操作。一个分子可能存在多个旋转轴（如BF3分子有1个C3轴和3个C2轴），其中n最大者称作主轴。

（2）反映

将分子中各点移至某一平面另侧等距离处后能够得到分子等价图形的操作称反映，用表示；进行反映所借助的平面称对称面，记作。由于反映操作实际上是把分子对于贯穿分子中的一个平面取镜象，对称面又可称镜面。一个对称面能产生两个对称操作：进行奇数次反映相当于一次反映

        （k=0，1，2，……）

进行偶数次反映相当于恒等操作

根据平面和旋转轴的位置关系（见图4.2），对称面分为三类：包含主轴的对称面记为，垂直主轴的对称面记为，包含主轴且平分垂直于主轴的两个C2轴夹角的对称面记为。

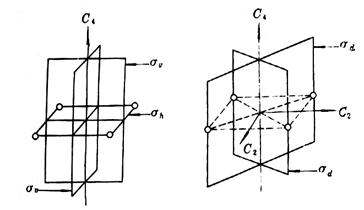
图4.2 对称面与对称轴关系示意图

（3）反演

选取分子的中心为笛卡儿坐标原点，把分子中任何一点（x, y, z）换到另一点（-x, -y, -z）后能得到分子等价图形的操作称反演，用表示。进行反演所凭借的中心点称作对称中心或反演中心，记作。与反映类似，一个对称中心只能产生两个对称操作：

    （k=0，1，2，……）

苯、二氧化碳等是具有对称中心的分子。

（4）象转

先将分子绕某轴旋转角度后，再凭借垂直于该轴的平面进行反映，如能够产生分子等价图形，这样的对称操作称象转，记作，相应的对称元素称象转轴，用Sn表示。显然象转是旋转和反映的复合操作，先反映后旋转和先旋转后反映是等价的，结果相同，即

在分子中，如果有一个Cn轴和一个与之垂直的，则必存在一个Sn轴，Sn就是Cn轴。但有的分子中既不存在Cn轴，也不存在与之垂直的，仍可以有Sn轴。如图3.3中的丙二烯分子，既不存在C4轴，也没有垂直于C4轴的，但却存在一个S4轴。

应该指出的是只有偶数次象转轴才是独立的对称元素，奇数次象转轴S2k+1不是独立的对称元素，先看看进行2k+1次象转操作的结果

这说明有S2k+1轴的分子必然含有，也就必然含有与垂直的C2k+1轴，这样S2k+1轴就与C2k+1轴重合，而不是独立的对称元素。

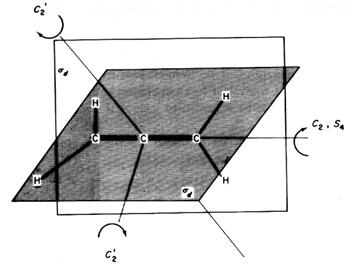
图4.3 丙二烯的对称元素