1.群的定义

设有一组元素的集合，定义一种称之为“乘法”的运算，如果满足下列条件，则集合G构成群：

具有封闭性，G中任何两个元素A和B的乘积R=AB都在这个集合中。

集合G中的元素满足乘法结合律，即(AB)C=A(BC)。

集合中存在一单位元素E，它与G中任何元素相乘都得该元素本身，即ER=RE=R。

集合G中任何一个元素R都有一逆元素R-1,且RR-1=R-1R=E。

下面对群的定义做一些说明：（1）群中的单位元素和每个元素的逆元素都是唯一的；（2）群中的元素是广泛的，可以是数、物理动作、对称操作和矩阵等等；（3）群元素之间的“乘法”是广义的，根据定义不同而有不同的意义。如全体整数（包括零）对数学上的加法构成群。在这里群元素之间的乘法就是代数上的加法。又如，四个动作立正、向左转、向后转和向右转构成群，这里定义的群元素之间的乘法就是一个动作之后接做另一个动作。

群中元素的数目叫做群的阶。上面提到的加法群是无穷阶群，而四个转向动作构成的群是四阶群。这两个群还有一个共同特点，就是群元素之间满足交换律，即AB=BA，这样的群称作对易群或阿贝尔群（Abelian group）。

2.分子的点群

如果定义对称操作的“乘法”为一个操作后进行另一个操作，那么一个分子全部对称操作的集合构成群。这种群称分子的对称操作群。因为对有限大小的分子施行所有的对称操作时，分子图形中至少有一点不动，这样的操作称作点操作，所以分子的对称操作群又叫做点群。根据分子中旋转轴的不同，可将常见的分子点群分成以下几类：

（1）轴向群

群：属于群的分子只有一个n次旋转轴，群元素有n个： 。（需要注意的是点群的元素是对称操作。为了书写方便，一律把对称操作符号中的“”号去掉，但不要把它与对称元素混淆了）。例如CHFClBr属C1群（分子无任何对称元素，只有一个恒等操作），H2O2 属C2群，而非交叉非重叠的CH3-CCl3属C3群。

群：分子有一个n次旋转轴和n个包含该轴的对称面就属于群，群元素有2n个： 。H2O属C2v群，NH3属C3v群，无对称中心的线形分子（如HCl）属群。

群：分子有一个n次旋转轴和一个垂直于该轴的对称面属于群。因为，所以属于群的分子有对称元素Sn，当n为偶数时还有对称中心。由于和可对易，故群有2n个群元素： 。反式的CHCl=CHCl属C2h群。只有一个对称面而没有其它任何对称元素的分子（如HOCl）属C1h群，一般用Cs表示。

群：分子有一个n次向转轴，属于群。这里n为偶数，因为n为奇数时，群就是Cnh群，不独立存在。群有n个群元素：  。椅式环己烷属S6群。反式CHClBr-CHClBr属S2群，群元素为，S2群通常记为Ci群。

（2）二面体群

群：有一个次的主轴和n个垂直于主轴的2次旋转轴的分子属于群。群有2n个群元素： 。部分交错式的CH3-CH3 属于D3群。

群：除具有群的对称元素外，还有一个垂直于主轴的对称面，这样的分子属于群。由于对称操作和可对易，故群有4n个元素：  。乙烯（CH2=CH2）分子属D2h群，三氟化硼（BF3）属D3h群，平面四方形的PtCl42-属D4h群，具有对称中心的直线分子（如CO2）属群。

群：在群的对称元素基础上加上n个对称面，这样的分子属于群。由于，该群有4n个群元素：    。丙二烯（CH2=C=CH2）属D2d群，交错式乙烷（CH3-CH3）属D3d群，交错式二茂铁属D5d群。

（3）立方群

分子有多个高次旋转轴（）时属这类点群，这里主要介绍其中最常见的两个。

Td群：具有正四面体构型的分子（如CH4，CCl4，SiH4）属Td群。分子的对称元素有4个C3轴，3个C2轴，3个S4 轴（与3个C2轴重合）和6个平面。Td群有24个对称操作分成5类：。

Oh群：具有正八面体构型的分子（如SF6，[PtCl6]2-，Mo(CO)6，[Fe(CN)6]3-等）属Oh群。分子的对称元素有3个C4轴，4个C3轴，6个C2轴，3个平面，6个平面，3个S4 轴，4个S6 轴和对称中心。Oh群有48个对称操作分为10类：。

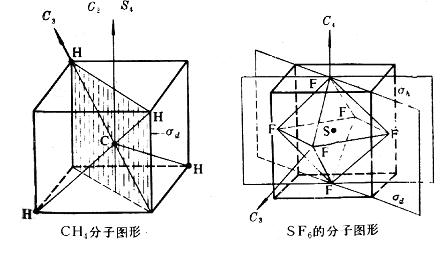
图4.4 CH4和SF6分子对称元素示意图

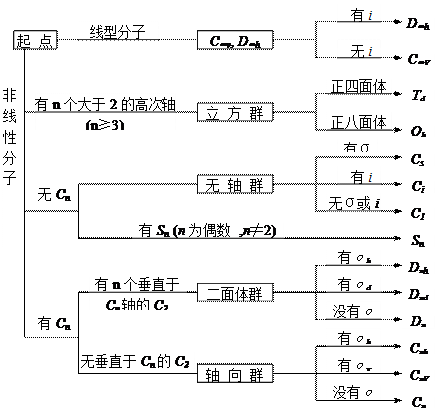
以上介绍了一些常见的分子所属的点群，对于一个给定的分子，可用表3.1判断它所属的点群。

表4.1 分子点群的确定步骤

 

3.群的乘法表

点群的元素之间的“乘法”定义为一个操作后接另一个对称操作。由于群具有封闭性，群中任意两个元素的乘积仍然属于这个群，因此只要知道了一个h阶群的所有元素，就可以排列出该群的乘法表。如图4.5所示的NH3分子属C3v群，有6个对称操作：，表4.2为C3v群的乘法表。

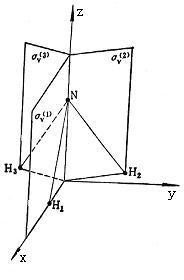
图4.5 NH3分子的对称性

表4.2 C3v群乘法表

由表4.2可知，h阶群的乘法表由h行和h列构成。表中上方横行中所列操作为第一操作，左方直列所列操作为第二操作。在横行第Ri个操作和直列第Rj个操作的交叉点上找到的操作是两个操作的乘积RjRi。由于对称操作的乘法一般不满足交换律，即，所以应注意两个对称操作相乘的次序。例如表3.2中横行的第五个元素σv(2)和直列的第三个元素C32相乘为C32σv(2)= σv(3)；而横行第三个元素C32和直列第五个元素σv(2)相乘为σv(2)C32 = σv(1)。

从C3v群的乘法表可以看出，群中的每个元素在乘法表的每一行和每一列中只出现一次，乘法表中不可能有两行或两列完全相同。每一行和每一列都是群元素的重新排列。

借助C3v群的乘法表，我们可将群中的元素进行分组，为此先引入相似变换概念。

若X和A是群G中的两个元素，且有

X-1AX=B                         (4-1)

B叫做A借助于X所得的相似变换，并称A和B是共轭的。将上式左乘X右乘X-1，得

X-1BX=A                         (4-2)

可见B也与A共轭。群中相互共轭的元素的集合称作共轭类，简称类。可见类是群中比群更小的集合。

由C3v群的乘法表可知E-1=E，C3-1=C32，σv-1=σv。我们用群中所有元素对C3进行相似变换，

EC3E= C3，C32 C3 C3= C3，C3 C3 C32= C3

σv(1)C3 σv(1)=C32，σv(2)C3 σv(2)=C32，σv(3) C3 σv(3)= C32

可得C3和C32为一类。同理可得E自成一类，σv(1)、 σv(2)和 σv(3)为一类。

4.分子的偶极矩和旋光性的预测

分子构型的对称性可用点群来描述，它反映出分子中原子核和电子的分布状况。因此分子的某些物理性质必然与分子的对称性有一定的联系。利用分子的对称性可对分子的偶极矩和旋光性做出简单直观的预测。

（1）分子偶极矩的预测

分子偶极矩的定义是分子正负电荷重心间距r与电荷量q的乘积，其方向规定为从正到负

μ=qr

偶极矩属分子的静态物理性质，其特点是对分子施行对称操作不会改变它的大小和方向，因为分子的对称性反映出原子核和电子云空间分布的对称性，分子正负电荷重心必定处于对称元素上，即偶极矩必须坐落在分子的对称元素上。如果分子有n次旋转轴，则偶极矩必位于该轴上；如果分子有一个对称面，则偶极矩必位于此面上；当分子有多个对称面时，则偶极矩必位于它们的交线上；如果分子有两个对称元素相交于一点（如有一个Cn轴和一个面）那么偶极矩只能位于两个对称元素的交点上，由于在该点上正负电荷重心间距|r|=0，或偶极矩向量大小|μ|=0。由此可以得到分子是否具有偶极矩的对称性判据：若分子中有两个或两个以上的对称元素交于一点，该分子必无偶极矩，否则就有偶极矩。

根据以上对称性判据，可推测属于下列点群的分子有偶极矩：C1群（如CHFClBr），Cs群（如HOCl），Cn群（如H2O2），Cnv群（如H2O，NH3），而属于Ci，Sn，Cnh，Dn，Dnh，Dnd，Td和Oh群的分子无偶极矩。

（2）分子旋光性的推测

如果某种物质能够改变偏振光的偏振方向就称这种物质具有旋光性或光学活性。旋光异构现象是有机立体化学的一个重要特征。

具有旋光性的化合物的特点是分子与它的镜象是一对对映异构体，它们等同而非全同，犹如人的左手和右手，互为镜象而不能完全叠合，这样的分子又称手性分子。所谓非全同是指手性分子不能通过旋转操作或平移操作与其镜象完全叠合。

显然，分子是否能与其镜象重合与对称性有关。象转是旋转和反映的复合操作,反映可使分子变成自己的镜象，再经旋转Cn得到分子的等价图形，这个等价图形和原始图形是可以叠合的，以及对称操作Sn必可使分子与其镜象叠合。因此可得出分子有无旋光性的对称性判据：有象转轴Sn的分子无旋光性，无象转轴Sn的分子有旋光性。

由于,因此也可以说具有对称面，对称中心i和象转轴S4n（n=1,2……）的分子无旋光性，否则有旋光性。由此可推测属于C1，Cn，Dn点群的分子有旋光性。