一、 甲烷的离域、定域分子轨道

(1)离域分子轨道 在上一节中给出了分子在单电子近似下的哈密顿算符。对于甲烷分子，单电子算符为:

                     （5-1.1）

式中第二项为五个原子核对电子i的吸引势。单电子薛定谔方程中待求的-MO波函数和-MO能级是的本征函数和本征值。因此应是一可观测量。

若只考虑价轨道参与成键，中心碳原子和四个氢原子共计有八个价轨道。在构造甲烷的MO时，按照LCAO-MO三原则，首先要考虑的是对称性匹配原则。

实验已测出 CH4具有正四面体的几何结构，属Td 点群，如图5-1.1所示。中心碳原子的价轨道在Td 点群中按对称性分类， 属 A1 不可约表示，而、和属于T2不可约表示。因此，四个氢原子的1ｓ轨道需先构成具有A1 和T2 对称性的群轨道，再与碳原子对称性一致的价轨道线性组合成MO。当电子排布到这样的MO上时，将在整个分子范围内运动，而不局限于二原子之间，这样的MO称为离域MO。

图5-1.1   甲烷分子的几何结构

这样构造出的离域MO是：

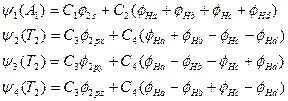              (5-1.2)

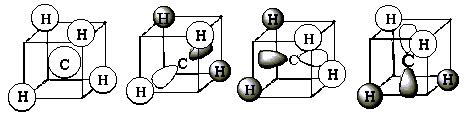
图5-1.2给出的是C1 或C3与C2或C4同正负号即成键离域MO的图形；此时四个MO分别满足A1 和T2 对称。若C1或C3与C2 或C4 正负号相反，则给出反键离域MO。这四个MO分别满足A1 和T2 反对称。

 (A1)      (T2)      (T2)      (T2)

图5-1.2   甲烷四个成键离域MO图形 (黑、白色分别代表正和负)

把、、和分别代入CH4分子的单电子薛定谔方程，解得的轨道能级如图5-1.3所示。

 

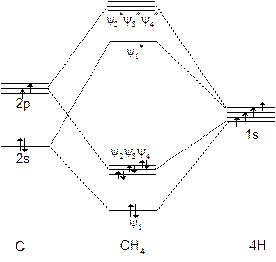
图5-1.3   甲烷离域 MO能级图

由光电子能谱测出的CH4价电子的电离能IP1＝23eV, IP2＝IP3＝IP4＝12.7eV，与离域分子轨道方法推出的结果一致。故称离域分子轨道为正则分子轨道。 

其它多原子饱和分子可用同样的方法去构造对称性匹配的离域分子轨道。

(2)定域分子轨道  根据量子力学的态叠加原理，若5-1.2式中四个离域分子轨道描述了甲烷中单电子的可能状态，那么由它们线性组合成的新波函数也应是描述甲烷分子中单电子的可能状态。

现设C1＝C3、C2＝C4，按5-1.3式进行线性组合可得与碳原子和一个氢原子价轨道相关的分子轨道。

            (5-1.3)

电子排布在这样的MO上，只分布在二个原子周围，所以5-1.3式波函数被称为定域MO。图5-1.4给出了这四个定域MO的轮廓图。

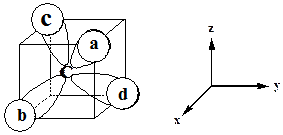
图5-1.4   CH4 中四个定域MO的轮廓图

图5-1.5给出CH4定域MO的能级图，可知成键MO和反键MO都是四重简并的。

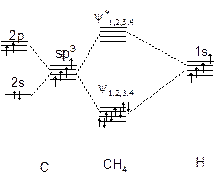
图5-1.5   CH4定域 MO能级图

实验不仅测得CH4的每个C-H键键长一样，键角一样，而且每个C-H键的离解能和极性都一样。这说明每一对碳氢原子间的电子云分布完全一样。按照经典化学键的语言来描述，这四个C-H键除取向不同外是完全等价的。我们看到由5-1.4式MO描述的正是这种化学键。

因此定域MO可以通过离域MO间的某种线性组合来得到，定域化学键的电子云可视为离域键电子云总密度按各对成键原子所占据的空间重新分摊的结果。离域MO模型的结果适于讨论与单电子行为有关的性质，如光谱、电离能及化学反应机理等；而定域MO模型的结果适于讨论与两成键原子间电子云密度统计结果有关的性质，如前所提及的键长、键能、键偶极矩等。

二、 杂化轨道理论

CH4定域MO的波函数和图形表明，中心碳原子的价轨道先线性组合成与某方向上的氢原子1ｓ轨道对称性匹配和满足最大重叠原理的新原子轨道而后组合成定域MO。这种原子处于价态的新原子轨道被称为杂化轨道。

(1)杂化轨道构造三原则若以｛｝表示某原子参加杂化的原子轨道集合，为杂化轨道，则：

  i=1，2，3……n                  (5-1.4)

(ａ)杂化轨道要满足归一化条件  杂化轨道是一种原子轨道,它描述了处于价态原子中单电子的可能状态。归一化的数学表达式为:

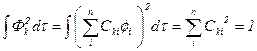              (5-1.5)

上面的计算用到了同一原子中原子轨道间满足正交、归一的条件。为在第k个杂化轨道中的组合系数，而表示在中的成分。

当把轨道中 s轨道的成分记为、p轨道的成分记为时，就有：

                                    (5-1.6)

                        (5-1.7)

(ｂ)参加杂化的轨道贡献之和为1   参与杂化的轨道是归一化的，杂化后在新形成的所有杂化轨道里的成分之和——即电子“分散”到各杂化轨道中的几率之和应为1。故有：

                                 (5-1.8)

由5-1.5和5-1.8式可知，有ｎ个轨道参与杂化应得ｎ个杂化轨道。

(ｃ)同一原子中杂化轨道间正交，正交的杂化轨道间排斥作用能最小，使原子体系稳定。按正交的定义有:

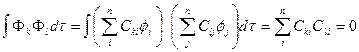      (5-1.9)

(2) s-p型杂化对于s-p型杂化轨道, 可写成:

                    (5-1.10)

若定义轨道的杂化指数为:

                           (5-1.11)

被称为是型杂化轨道。若两杂化轨道间杂化指数相同，称为等性杂化轨道；否则反之。若原子中所有杂化轨道的指数都相同，则称该原子发生了等性杂化。

为进一步讨论的需要，定义归一化的组合 p轨道为：

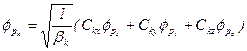      (5-1.12)

Fk可改写成:

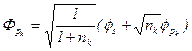                  (5-1.13)

显然的极值指向就是Fk的极值指向，Fk和Fl极值指向间的夹角qkl，就是成键后的键角。

根据相关的数学知识有:

                         (5-1.14)

利用Fk和Fl间正交，可导出:

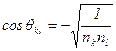                           （5-1.15）

（ａ）s-p等性杂化  表5-1.1列出了三种s-p等性杂化。

表5-1.1  s-p等性杂化

 

轨道数    a     b     ｎ    q     杂化形式    Fk的空间分布

 

2      1/2   1/2    1    180°     sp           直线型

3      1/3   2/3    1    120°     sp2          正三角型

4      1/4   3/4    1   109o28′   　 sp3          正四面体型

 

对于采用sp3杂化的碳原子，若取杂化轨道Fl的极值指向图5-1.1中C-Ha键方向，此时归一化的组合ｐ轨道为

                         (5-1.16)

     (5-1.17)

该结果与5-1.3式里CH4 定域分子轨道中相关部分完全一致。可推出另三个杂化轨道波函数与余下三个定域MO中相关部分也完全一致。

对于采用sp2等性杂化的原子，若取极值指向X轴正向，则。故:



当取和在XY坐标面上时，三个杂化轨道在XY平面上的取向加图5-1.6所示。

由图解可得：



在BF3分子中,B原子就采用此种杂化轨道与F原子形成定域MO，构成平面三角形分子。

 

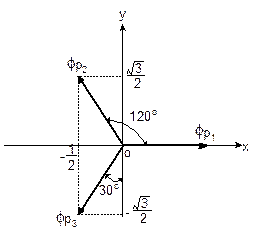
图5-1.6  sp2组合p轨道的极值取向

(ｂ) s-p不等性杂化  Ｈ2Ｏ分子中二个氢氧键键长、偶极矩等性质都一样，可认为氧原子用二个等性杂化轨道F1、F2参与成键。实验测得水分子键角为104.5°，所以杂化指数可由 5-1.15式求得：

-1/n ＝cos104.5°＝-0.25

得ｎ＝４,氧原子采用sp4杂化轨道成键。从5-1.13式可推导出杂化轨道波函数: 



可知a1,2＝0.2, b1,2＝0.8。若要进一步求轨道的具体波函数，只要选定F1,2 所在的平面( H2Ｏ分子所在平面)和其中一轨道的具体指向(H-O键的指向)，就可求得。

NH3 分子具有四面体结构，三个N-H是等价的。因此氮分子采用三个等性杂化轨道参与成键。实验测得∠HNH＝107°，可求得杂化指数ｎ＝3.42，即为sp3.42 杂化。因ｎ＝b／a，a+b＝1，可得 a＝0.226，b＝0.774。即：

      (ｋ＝１，２，３)

氮上孤对电子占据的杂化轨道φs,as＝1-3a＝0.322，bs＝3-3b＝0.678，得ｎs＝2.1，为sp2.1杂化轨道。

 

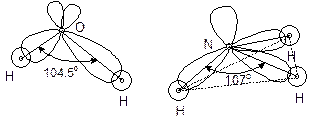
图5-1.7   气态 H20(a)和 NH3(b)分子中的不等性杂化

(3)价电子对互斥原理(VSEPR)  CH4、NH3 和H2O的中心原子C、Ｎ、Ｏ都用了2s和三个2p轨道参与杂化， 因价电子数不同造成孤对电子数和成键数不同。由于孤对电子占据的杂化轨道中的s轨道成分大，电子云分布比成键电子的更靠近中心原子，因此各类电子对间的静电排斥作用大小的顺序为：

孤对-孤对＞孤对-键对＞键对-键对

这样从价电子对间的静电排斥作用也可推测CH4应是正四面体结构,CH4、NH3、H2O键角大小顺序为：

CH4＞NH3＞H2O

用此法去推断多原子分子的构型是很有用的，被称为价电子对互斥原理。

由于d电子参与杂化的情况比较复杂，表5-1.2给出有关等性杂化的类型和空间构型。

表5-1.2   有ｄ轨道参与的等性杂化

杂化轨道数       杂化类型       杂化轨道分布的空间构型

2         dp              直线形   　　　　 　       sd              弯曲形    　　 3         dp2            　平面三角形    　　　　 　       d2s             平面三角形    　　 4         d3s           　 四面体形    　　　　 　       dsp2           　平面正方形    　　 5         dsp3          　 三角双锥形    　　　　 　       d3sp           　三角双锥形    　　　　 　       d4s            四角锥形    　　 6         d2sp3          　　正八面体形    　　　　 　       d4sp            三棱柱形