共轭分子与饱和分子不同，不能用单一的经典结构式来描述，具有单、双键平均化的特征。共轭分子很难用定域MO模型来解释。休克尔(Huckel)提出一种简单而又有效的MO法—HMO法去讨论共轭体系，获得成功。

一、HMO法概述

(1)s-p 体系分离近似从第四章的讨论可以得知，只有共面的原子间可形成离域p 键。若该平面为XY平面，这些原子的轨道pz在 XY 平面反映下呈反对称,可线性组合成离域 p 轨; 与pz轨道相反，这些原子的ｓ、px、py 轨道呈对称, 可参与组成s 分子轨道。由于这二类AO对称性相反，不会有效组合成MO，可采用分离近似以简化共轭体系的处理过程。

(2)p 单电子近似若为 p 单电子哈密顿算符，由共轭骨架上原子的Pz轨道线性组合成的p 单电子试探波函数为,则p单电子薛定谔方程为：

                     (5-2.1)

式中E为p 轨道能。

(3)休克尔近似——休克尔方程及行列式 采用4-1节中的线性变分法处理p 单电子薛定格方程5-2.1式，可得久期方程组:

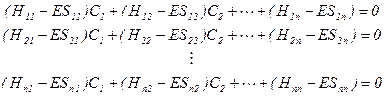     (5-2.1)  

休克尔对式中的积分元采取了如下近似：

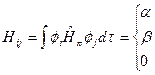
               (5-2.3)

           

式中库伦积分a 近似等于相应AO的轨道能，交换积分b 为一负常数。

采用由5-2.3式叙述的休克尔近似后，对于由同一种原子组成的直链共轭体系，久期方 程变成如下休克尔方程：

                            

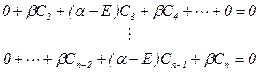                  (5-2.4)

进一步令 ，休克尔方程为：

cC1 + C2                  =0

　　　　C1 + cC2 + C3             =0        

　　　　　　　　　　　　　C2 + cC3 + C4       =0             (5-2.5)

　　　　　　　　　　　　　　.

　　　　　　　　　　　　　　.

　　　　　　　　　　　　　　.

　　　　　　　　　　　 Cn-1 +cCn  =0       

5-2.5式为线性齐次方程组，要有非零解休克尔行列式 必须为零。

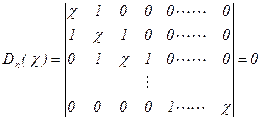           (5-2.6)

休克尔行列式展开是c的一元ｎ次方程，解有ｎ个c 的根，进一步可得由a 和b 表达的ｎ个离域p 轨道能E。

把ｎ个c 值依次代入休克尔方程(5-2.5式)，再加上休克尔近似下的归一化条件:

      (5-2.7)            

就可解出ｎ套离域p 轨道的线性组合系数｛Cki｝，即已求得。

二、丁二烯和链烯烃的解

(1)丁二烯 

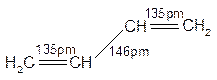
                  图5-2.1  丁二稀的结构

丁二烯的分子结构如图5-2.1所示。由碳2pz轨道组成的离域p -MO可写成:

从5-2.6式可推得丁二烯的休克尔行列式为:

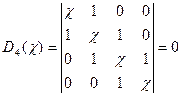                   (5-2.8)

展开可得(参看5-2.11式):

得解:

X＝±1.618，±0.618

p 轨道能由低到高为:

c＝ -1.618       E 1＝a+ 1.618b

c2 ＝ -0.618       E2 ＝a  + 0.618b

c3＝  0.618       E3 ＝a  - 0.618b

c4 ＝ 1.618       E4 ＝ a -1.618b

把c1 - c４ 分别代入丁二烯的休克尔方程(参看5-2.5式)再加上归一化条件(5-2.7式描述)，可得如下四组离域p-MO 波函数：

＝0.3177f1+0.6015f2+0.6015f3+0.3717f4

＝0.6015f1+0.3717f2-0.3717f3-0.6015f4

＝0.6015f1-0.3717f2-0.3717f3+0.6015f4

＝0.3717f1-0.6015f2-0.6015f3-0.3717f4           (5-2.9)

图5-2.2给出了丁二烯p -MO能级图，由此易算出共轭体系中p 电子总能量为：

EDp＝2E1+2E2＝4＋4.472                    (5-2.10)

 

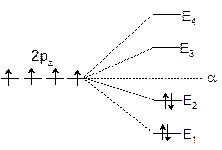
图5-2.2   丁二烯离域 p 轨道能级图

若按定域键的模式，两个p 键应分别定域在Ｃ1、Ｃ2和Ｃ3、Ｃ4间。则可得两个等同的二阶休克尔行列式:

     ＝0

展开为-1＝0，＝±1，E1＝+、E2＝。所以定域模型下丁二烯的四个p电子占据两个简并的定域成键p轨道,p电子总能量为：

ELp＝４×Ｅ1＝４＋４

比较EDp和ELp 可得丁二烯的离域能：

DEp＝EDp- ELp ＝0.472

因为负值，所以p 电子离域后可为分子带来稳定化能。对于其它共轭分子，定域模型下p 电子总能量算法同上。需要强调的是：若p 体系为自由基，未成对p电子能量应为。

(2)链状共轭烯烃对于有ｎ个碳的链状多烯烃，休克尔行列式具有5-2.6式。ｎ＞3后不能直接展开，而须采用数学上已证明的递推公式展开。

           (5-2.11) 

再加上已知，就可以得到的展开式 。

对于含ｎ个碳原子的链状多烯烃，其轨道能和MO系数的通解公式已得到。若ｊ为p-MO 的序数，为碳原子的序数，则：

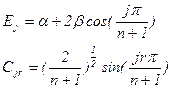     ｊ，ｒ＝１，２，……，ｎ       (5- 2.12)

三、 苯和环烯烃的解

(1)苯苯中碳采用sp2杂化成键，碳骨架呈平面六边形，它的休克尔行列式为：

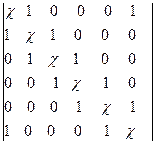  ＝0              (5-2.13)

可见，若单环共轭烯烃中碳序号按环中序取值时，休克尔行列式与链共轭烯烃不同之处为右上角和左下角行列式元不是0而是1。展开行列式可得(展开法请参看5-2.18式):



可得解:

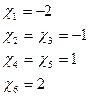
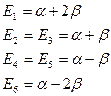                   (5-2.14)

相应的六个p-MO的波函数:

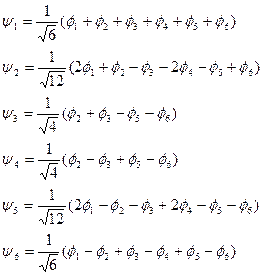           (5-2.15)

图5-2.4给出了苯p-MO能级图，由此易推出共轭 p 电子的总能量EDp和离域能DEp。

       (5-2.16)              因丁二烯的DEp＝0.472b，苯比它大四倍多。可见苯的共轭体系具有特殊的稳定性。

由图5-2.4可知y1是强成键MO，y2、y3是成键MO，y4、y5 是反键MO，y6 是强反键MO。

 

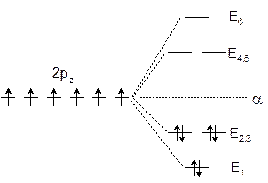
 图5-2.4   苯的p -MO能级图

(2)单环共轭烯烃对于有ｎ个碳的单环共轭烯烃休克尔行列式为:

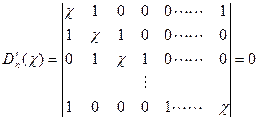          (5-2.17)

数学上已导出 与链共轭多烯休克尔行列式间存在如下关系

                  (5-2.18) 

即按的展开办法可得展开式。数学上已得到p -MO能级的通解公式： 

    ｊ＝0,１,２，……ｎ-1   (5-2.19)

Ｅｊ分布的规律性可用弗劳斯特 (Frost)图示法表示。该法先画以｜２b｜为半 径 的圆，对有ｎ个碳的单环共轭体系，过圆下顶点作内接正ｎ边形，各内接点表示一p-ＭＯ 能级。能量坐标为过下顶点与圆心的连线，圆心处为a ，下顶点为a＋２b。图5-2.5给出ｎ＝4 - 7单环共轭烯烃p -MO能级的弗劳斯特图示法。

图5-2.6显示，对于单环多烯CnHn 的p 能级分布为：最低能级是非简并的，其余次高能级均为二重简并，最高能级ｎ为奇数时简并、ｎ为偶数时非简并。一个稳定的单环共轭体系，p 电子体系应具备闭壳层结构,此时p 电子总数应满足：

np ＝4ｍ＋２         ｍ＝０，１，２，……           (5-2.20)

此即休克尔芳香性规律。

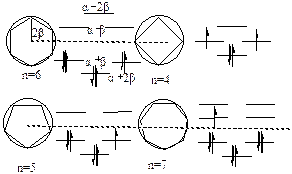
图5-2.6   单环共轭烯烃弗劳斯特图

实验上除发现苯具有特殊的稳定性外，环丙烯阳离子(C3H3+)、环戊二烯阴离子(C5H5-)和环庚三烯阳离子(C7H7+)都具有芳香性。这说明HMO法的合理性，也为后来迅速发展的半经验MO理论在化学中的应用奠定基础。

四、 分子图

HMO法对直链和单环共轭烯烃应用的成功表明，离域p键是决定该类分子性质的主要因素。下面将引入p 电荷离密qr、p 键级prs 和自由价Fr几个休克尔特征参量，来进一步描述共轭分子的物理化学性质。

(1)p 电荷密度 若p -MO   ，因在休克尔近似下，则Cjr2可认为是该轨道p 电子云分布在原子ｒ处的电荷密度。设ｎj为分子轨道yj 上排布的p 电子数，原子ｒ处总p 电荷密度为：

                       (5-2.21)

qr 也被称为原子ｒ上的p 电子布居数。

由5-2.9式可求得基态丁二烯四个碳原子上p 电荷密度为：

q1＝2×（0.3717）2 + 2×（0.6015）2＝1.000

q2＝2×（0.6015）2 + 2×（0.3717）２ ＝1.000

q3＝2×（0.6015）２ + 2×（-0.3717）２＝1.000

q4＝2×（0.3717）２ + 2×（-0.6015）２＝1.000

即丁二烯中每个碳原子拿一个2p电子参加共轭，共轭成键后每个碳原子统计得到一个p 电子的电荷密度，故形成的是非极性的离域p 键。苯分子具有同样的结果。

(2)p 键级在４-2节中曾定义了双原子分子的键级为净成键电子数的一半。实际上这是种定域键强度的描述，对离域p 键须另行定义。

把丁二烯的p -MO波函数与H2+ 的成、反键MO波函数进行比较可知，在5-2.9式中，若相邻原子r、s间线性组合系数同号表示原子间价电子云密度大、起成键作用，而异号时起反键作用。因此可用p -MO中相邻原子间组合系数乘积的符号和大小表示是成键或是反键作用及强弱。即相邻原子r、s间共轭p 键的总键级为：

                   (5-2.22)

nj 仍为yｊ中排布的p电子数,表示分子轨道yｊ中r、s原子间键级。

若定义r、s原子间s 键键级为1，则r、s原子间总键级:

 Prs = 1 + prs                              (5-2.23)

因此，由5-2.9式可算得丁二烯基态原子间总键级为：

P12＝P34＝1.894

     P23＝1.447

(3)自由价图5-2.7给出二亚甲基乙烯双基假想分子的经典结构。用HMO 法可解得中心碳原子与其余碳原子间的p 键级:

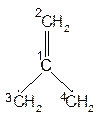
图5-2.7   二亚甲基乙烯双在分子结构

若定义共轭分子中r原子的总成键度:

                            (5-2.24)

则二亚甲基乙烯中心碳原子的总成键度:

可证明它是共轭体系中碳原子总成键度最大的情况。再定义算例分子中某碳原子的总成键度与4.732的差值为该原子的自由价，即：

Fr ＝ 4.732 - Nr                    (5-2.25)

则Fr 值表示ｒ原子剩余成键能力的相对大小。所以丁二烯中：

Ｎ１＝Ｎ4＝2+1.894＝3.894

Ｎ2＝Ｎ3＝1+1.894+1.447＝4.341

F１＝F4＝4.732-3.894＝0.838

F2＝F3＝4.732-4.341＝0.391

(4)分子图及其应用在分子的共轭骨架上，把电荷密度标在原子附近、键序标在成键原子间的连线上、自由价标在起点在原子的箭头方向上构成的图形叫分子图。对于共轭分子，分子图比通常的结构式更本质地表达了分子的性质。

图5-2.8给出了丁二烯和苯的分子图，是考虑了分子对称性后的简化图形。 

 

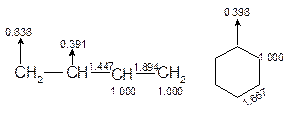
             （a）               (b)

图5-2.8   丁二烯(ａ)和苯(ｂ)的分子图

由图可知：(1)在丁二烯中，由于2＞P12＝P34＞P23＞1，可很好解释实验测定结果     LC＝C(定域)＜ LC1-C2 ＝ LC3-C4 ＜ LC2-C3 ＜LC-C (定域)和苯环键长平均化；(2)二分子都是非极性分子；(3)丁二烯中F１＝F4＞F2 ＝ F3，因此易发生1、4位加成反应；而苯中自由价一样且值较低，不易发生加成反应，加之离域能很负，十分稳定。

图5-2.9给出苯胺和吡啶分子图。两分子中N都采用sp2 杂化成键，但苯胺中N用一对孤对电子参加共轭，而吡啶中N用单p电子参加共轭。所以苯胺中N带净正p 电荷而吡啶中N带净负p 电荷，分子的离域p 键都具有极性。在已知键长、键角时，可求算离域p 键的偶极矩值。

有机共轭分子取代反应有自由基取代、亲电取代及亲核取代。由分子图判断反应发生的位置存在如下规律：

①自由基在自由价最大处发生反应；

②亲电、亲核基团分别在电荷密度最大、最小处发生反应；

③若电荷密度相同，均在自由价最大处发生反应。

若上两分子与亲电基团NO2+反应，按上规律取代反应位置对苯胺应发生在2、4、6位，而吡啶应发生在3、5位，与实验结果完全一致。若与亲电基团NH2-反应，反应应发生在吡啶的邻位，而自由基取代反应发生在邻、对位。

 

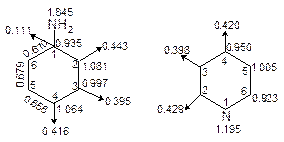
图5-2.9   苯胺(ａ)和吡啶(ｂ)分子图            

五、离域p 键形成的条件及分类

作为讨论共轭体系的HMO法，不仅适用于有机分子,也同样适用于无机分子。判断一个分子是否为共轭体系或具有离域p 键的条件有二个：一是共轭部分原子必须共面且有垂直于该平面的ｐ轨道；二是参加共轭的p 电子数必须少于共轭原子数的二倍，以保证净成键电子数大于零。离域 p 键的符号为 ，ｍ为参加共轭的原子数或轨道数，ｎ为p 电子数。离域 p 键可分为三种：

(1)ｎ＜ｍ，缺电子离域p 键。如图中的丙烯基阳离子。由于它可以是稳定的反应中间体，所以Ｈ2Ｃ＝ＣＨ-ＣＨ2Ｃｌ易发生离子型反应。

(2)ｎ＝ｍ，等电子离域p 键或正常离域p 键。如丁二烯、苯、萘等稳定共轭分子。另如NO2具有V型结构，具有一个键。

(3)ｎ＞ｍ，多电子离域p 键。共轭体系中含有多电子原子——N、O、F和Cl等时易形成多电子离域p 键，也有负离子的情况，比较复杂。值得一提的是与H2Ｃ＝ＣＨ-ＣＨ2Ｃl中的Cl较活泼不同，氯乙烯因形成，使Cl呈现明显的化学惰性。

六、 HMO法的局限性

HMO法对共轭体系的应用获得成功，但它又具有明显的局限性和不足。

(1)它被局限于只适用平面型共轭体系，且不包括s 体系，不能对分子的整体结构和性质进行讨论。

(2)由5-2.3 式描述的休克尔近似是相当粗糙的，特别是其中忽略全部原子间的重叠积分和不相邻原子间的交换积分，只可能获得定性结果。

考虑到HMO法图像清晰，计算十分简单和讨论共轭体系一般规律的适用性，它应是MO理论初学者须掌握的重要内容。