配位化合物是指由中心金属原子或离子(M）及周围若干配体（L－分子或离子）组成的化合物（MLn），并把金属与配体间的化学键称为配位键。

目前研究配位键的理论包括晶体场理论、分子轨道理论及在此基础上发展起来的配位场理论。

一、 晶体场理论

晶体场理论把配合物中中心金属与配体间的相互作用视为类似于离子晶体中正、负离子间静电作用，晶体场理论研究的主要对象是过渡金属离子配合物。该理论认为：中心金属原子原五重简并的d轨道在配体负电荷场的静作用下要发生能级分裂，从而引起d电子重新排布。由此成功地讨论了这类配合物在光谱、磁性、热力学和立体结构等方面的特殊性质。

1. d轨道在晶体场中的能级分裂  

六配位和四配位是过渡金属离子配合物的主要形式。若把配体视为负的点电荷，配体将分别形成具有Oh，Td和D4h点群对称性的晶体场，分别称为正八面体场，正四面体场和正方形场。这样，中心金属原五重简并的d 轨道由于它们在空间的取向（轨道极值的方向）不同，受到晶体场的作用也不同，发生能级分裂。

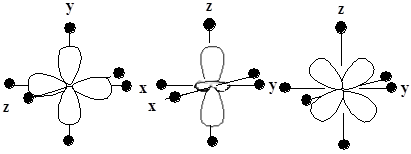
以六配位的配合物为例，图6－1.1给出了5个d轨道的电子云在Oh场中的取向。按Oh点群的特征标表，和属于eg不可约表示，电子云极值指向配体，受晶体场的作用强，能级记为；而、和轨道的属于不可约表示，电子云极值指向配位连线的中点，受Oh场作用相对要弱，能级记为。若把配体相应的电荷平均分布于正八面体所在的外接球面上时，所形成的场称为球形场，此时d 轨道能级升高但仍为五重简并，用表示，并取为能量的原点，则三者能量间关系可由6－1.1式表示：

－＝D0＝10

2+3=5=0      (6-1.1)

(a)            (b)              (c)

图6－1.1  五个d轨道电子云在Oh场中的取向

(黑球为配体；中间为d轨道的电子云; 、和情况同,只需旋转坐标轴。)

式中D0称为d轨道在Oh场中的分裂能，用10来表示。图6－1.2描述了d轨道在Oh场中分裂的推算和结果，得=6，=-4。

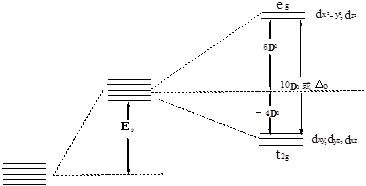
自由离子   球形场         正八面（Oh）场   

d轨道

图6－1.2  d轨道在Oh场中的能级分裂

对于Td场和场，由其特征标表可知，5个d轨道所属的不可约表示及分组情况与Oh场不同，因此分裂情况发生变化。5个d轨道在缺少对称中心的Td场中分组情况与Oh场类似，但能级顺序正好相反。场中，配体的平面配位正对轨道的四个极值，使它的轨道能级明显上升，5个d轨道分裂成四组。图6－1.3给出了它们能级分裂的图示

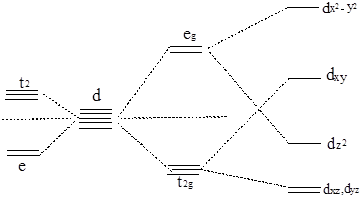
  正四面体场  球形场  正八面体场      正方形场

图6－1.3  d轨道在晶体场中的能级分裂。

2. d电子的重新排布 

在自由金属原子和离子中，d轨道是五重简并的，电子的排布遵循洪特规则。在晶体场中，d轨道的能级分裂使其不再具有五重简并的特点，d 电子将重新排布。以正八面体配合物为例，d 电子重新排布由分裂能D0和电子成对能P 的取值来决定。这里电子成对能是指使原本自旋平行单占据二个简并轨道的电子被迫挤占同一轨道时所需的能量。

为描述d电子重新排布带来的化学键效应，晶体场理论提出用晶体场稳定化能（CFSE）来讨论：

CFSE＝－                       （6-1.2）

式中，为球形场中d电子的总能量，通常取为能量坐标的原点; 为d电子重新排布后的总能量。现以在Oh场中中心金属是d4组态为例进行讨论。d4组态在Oh场中d电子有二种可能的排布方式：A：;  B：。

CFSE(A) = －(4´+P) = 16－P

CFSE(B)= －(3´+) )= 6

CFSE(A)－CFSE(B) = 10-P = D0－P

即：D0>P时，A排布方式稳定，d电子采用低自旋排布，对应的晶体场称为强场; 当D0<P时，B排布方式稳定，d电子采用高自旋排布，对应的晶体场称之为弱场。

对于正四面体配合物，由于配体只有四个，使Td场都是弱场，d电子采用高自旋排布。

由6-1.1表可见，对于八面体配合物当中心金属处于d4－7组态时，在强和弱场中未成对电子数有明显区别，使配体不同时同种中心金属原子或离子配合物的磁性差别显著。如配位离子[Fe(H2O)6]2+和[Fe(CN)6]4－的中心金属都为Fe2+离子（d6组态），但前者显强顺磁性而后者显反磁性，说明配体H2O对Fe2+形成的Oh场为弱场，而配体CN- 对Fe2+形成的Oh场为强场。在总结大量实验现象的基础上，d轨道分裂能随配体改变而变化的大致次序为：

I－<Br－<Cl－<SCB－<OH－~NO2－~Ac－<C2O42－<H2O

<EDTA<吡啶~NH3<乙二胺<联吡啶<NO2－<CN－~CO

由于分裂能值通常从配合物的光谱来确定，故该次序称为光谱化学系列。

表6-1.1   八面体配合物中d电子的重新排布和CFSE。

	弱场			强场
组态	排布	未成对 电子数	CFSE	排布	未成对 电子数	CFSE
d1 d2 d3 d4 d5 d6 d7 d8 d9 d10	t2g1 t2g2 t2g3 t2g3eg1 t2g3eg2 t2g4eg2 t2g5eg2 t2g6eg2 t2g6eg3 t2g6eg4	1 2 3 4 5 4 3 2 1 0	+4Dq +8Dq +12Dq +6Dq 0Dq +4Dq +8Dq +12Dq +6Dq 0Dq	t2g1 t2g2 t2g3 t2g4 t2g5 t2g6 t2g6eg1 t2g6eg2 t2g6eg3 t2g6eg4	1 2 3 2 1 0 1 2 1 0	+4Dq +8Dq +12Dq +16Dq－P ＋20Dq－2P +24Dq－2P +18Dq－P +12Dq +6Dq 0Dq

（3）配合物的光谱、水合热及几何结构特征   配合物中心金属的d轨道分裂后，在光照下d电子可从能级低的d轨道跃迁到能级高的d轨道，产生d－d跃迁和吸收光谱，所吸收的光子能量应等于分裂能。由于d－d跃迁对应的光子频率在近紫外和可见光区，故过渡金属配合物通常都有颜色。应注意配合物显示的颜色为吸收光的补光。如配位离子 [Ti(H2O)6]3+ 在20400cm-1 处有一吸收带，对应可见光谱的蓝绿区，所以配位离子 [Ti(H2O)6]3+ 的颜色为其补色淡紫色；而分裂能D0即为波数等于20400cm-1光子的能量。

第一系列过渡元素二价离子由Ca2+到Zn2+与H2O形成八面体配合物[M(H2O)6]2+时，按元素周期律的规则，随着核电荷数的递增，从Ca2+到Zn2+的离子半径应递减，使水化热循序上升，对原子序数做图应为平滑曲线。但在[M(H2O)6]2+中，第一系列过渡金属二价阳离子与配体H2O间的水化热除了上面提及的正常化学键效应（图6－1.4中平滑线）外，还应加上金属离子内d电子重新排布带来的晶体场稳定化能。实验测定发现，为双峰根据光谱化学系列，

由H2O配位形成的Oh场应是弱场。从表6－1.2可知，CFSE由Ca2+到Zn2＋时呈双峰型，与平滑曲线加和就是图6－1.4的双峰曲线。很好地解释了水化热产生偏差的原因。实验上发现第一系列过渡元素三价离子的水化热曲线和二价离子卤化物的晶格能曲线也呈双峰型，同样可由弱场中d电子的CFSE取值规律来解释。

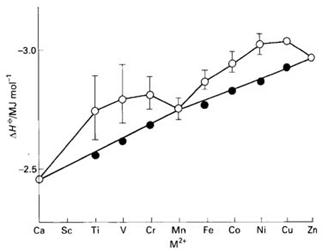
图6－1.4  第一系列过渡元素M2＋水化热双峰曲线

表6-1.2 Cu2+ 化合物晶体中的金属-配体间距离（单位：nm）

化合物	平面方向	轴向
CuF2	0.193	0.227
CuCl2	0.230	0.295
CuBr2	0.240	0.318
Cu(HCOO)2×4H2O	0.200	0.236
[Cu(NH3)6]2+	0.207	0.262

实验发现，六配位的过渡金属配合物的构型许多都是变了形的八面体，而不是正八面体。表6－1.2列出了一些Cu2+化合物晶体中Cu2+处于六个阴离子构成的八面体中心时金属-配体间的距离。由表可看出，对应的配位八面体中有的一个轴比其它二个轴长，呈拉长型；有的一个轴比其它二个轴短，呈压缩型。按晶体场理论，电子组为d9的Cu2+离子，在强、弱Oh场中d电子都为方式排布，但由于组轨道由和二个轨道组成，所以三个d电子可有二种排布方式; (A) ,(B) 。考虑到电子云的极大值指向z轴上的二个配体（在晶体场中视为负点电荷），而的电子云极大值指向x、y轴上的四个配体。因此，电子采用A式排布时，z轴上二配体受到d电子云的排斥就要大于另四个配体，配合物的平衡构型则呈拉长型;而当电子采用B式排布时，配体受d电子云排斥情况正与A式相反，配合物平衡构型则呈压缩型。配合物这种发生了变形的现象称为姜－泰勒效应（John-Teller effect）。表6－1.3列出八面体发生变形的d电子结构，其它情况具有理想八面体构型。

表6－1.3  八面体发生变形的d电子结构

	高自旋	低自旋
小畸变	(t2g)1,(t2g)2,(t2g)4(eg)2,     (t2g)5(eg)2	(t2g)1,(t2g)2,(t2g)4,(t2g)5
大畸变	(t2g)3(eg)1, (t2g)6(eg)3	(t2g)6(eg)1,(t2g)6(eg)3

二、 配位场理论简介

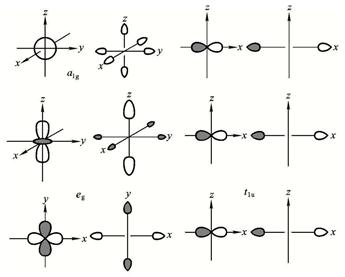
图6-1.5 满足 s 对称性的金属AO和配体对称性匹配的群轨道

晶体场理论主要考虑配合物中金属与配体间的静电库伦作用，着重讨论金属的d轨道在晶体场中分裂后d电子重排带来的特殊化学键效应，成功地解释了配合物的d-d跃迁光谱、磁性、水合热及几何结构的变形等重要特性，而在配合物理论中占有重要地位。

但由于晶体场理论忽略了金属与配体间相互作用的共价键效应，使该理论存在明显的欠缺。如在配体的光谱化学系列中，卤素离子形成的晶体场为什么倒会比中性分子NH3、H2O的弱？金属原子与极性很小的CO间形成的羰基配合物为什么稳定？一些不饱和的有机配体为什么在配合物中化学反应活性明显增加（络合催化）？

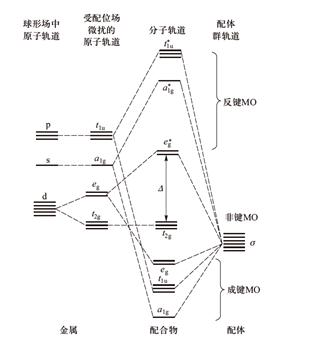
图6-1.6 配合物中的离域 s-MO能级图和分裂能

另外，有关实验也证实在配合物的配体上存在金属d电子云的分布，说明金属与配合物间有电子的交换。因此，研究配合物的完整理论不仅应有晶体场理论部分，还应有分子轨道理论部分。 配位场理论就是这二种理论的有机结合。下面以八面体配合物ML6为例进行介绍。在八面体配合物中，中心金属的八个价轨道在Oh点群中分属四个不可约表示。ns 属a1g、np属t1u、（n-1）d属 和不可约表示。其中ns 、np 和 不可约表示的6个AO 与M-L键呈轴对称，可由LCAO-MO方法与配体满足对称性匹配的轨道进行有效的组合形成离域的 s-MO。这样，须先把6个配体满足M-L轴对称的 s 轨道组合成与金属相应轨道对称性匹配的群轨道，再进一步组合成配合物的离域 s 轨道。由于金属的三个组d轨道在配合物离域 s-MO形成过程中为非键轨道；而在形成的反键 s 离域轨道* 中，金属的d轨道成分大，可以近似视为d轨道。所以配位场理论把 组和* 组轨道间的能级差作为晶体场理论中的分裂能D0，从而含纳了晶体场理论的核心内容。

   

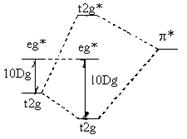
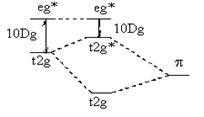
金属   配合物    配位体     金属   配合物    配位体

（a）                        (b)

图6-1.7  配位体分别用（a）p*空轨道和 (b) p占据轨道与

中央金属间离域 p 轨道的形成及对分裂能的影响

M和L间除了可形成 s 离域轨道外，由于M还有满足过M-L键平面反对称的组d轨道，若配体也有满足这种 p 对称性的轨道（如处于Z轴上卤离子的、轨道， CN-或CO的2p轨道），M和L间可进一步形成离域 p 轨道。但由于卤离子的 p轨道能要明显低于 CO和 CN-的反键 p 轨道能，而金属的组d轨道能居中，使新形成的反键 p 轨道*中d轨道成分多，使分裂能比仅形成离域s 键时有所降低，故卤离子是弱场配体。对于CO和 CN-的反键 2p 轨道，情况正好相反，使新形成的成键的离域 p 轨道中d轨道成分多，增大了分裂能，成为强场配体。由于H2O和NH3 没有满足生成离域 p 轨道的轨道，形成的配位场强度居中，很好地解释了配体的光谱化学系列次序。