1.晶体概述

晶体及其特性  晶体是由原子（离子、分子）或基团（分子片断）在空间按一定规律周期重复地排列构成的固体物质。晶体中原子或基团的排列具有三维空间的周期性，这是晶体结构的最基本的特征，它使晶体具有下列共同的性质：可自发地形成多面体外形，具有均匀性和各向异性。 晶体具有明显确定的溶点、对称性、对X射线衍射等特性。另外，晶体还有一种非常重要的唯其独有的性质——晶体中会存在缺陷，这是材料科学的基础。

2.晶体的点阵结构理论

晶体的点阵结构是实际晶体空间结构的数学描述形式。

点阵和结构基元

（1）点阵与平移  在晶体内部，原子或分子在三维空间作周期性地重复排列，如果在每个重复单位的相同位置定一个点，可得到一组点，这些点按一定规律排列在空间，研究这些点在空间重复排列的方式，可以更好地描述晶体内部原子排列的周期性。从晶体中无数个重复单位抽出来的无数个点，在三维空间按一定周期重复，它具有一种重要的性质：这些点构成一个点阵。点阵是一组无限的点，连结其中任意两点可得一向量，将各个点按此向量平移能使它复原，凡满足这条件的一组点称为点阵。

（2）结构基元  点阵结构中每个点阵点所代表的具体内容，包括原子或分子的种类和数量及其在空间按一定方式排列的结构，称为晶体的结构基元。将晶体结构示意表示为：晶体结构＝点阵＋结构基元。

（3）直线点阵  根据晶体结构的周期性，将沿着晶棱方向周期地重复排列的结构基元，抽象出一组分布在同一直线上等距离的点列，称为直线点阵。图7.1.1示出按一维周期排列的结构及其点阵。图中：（a）为NaCl晶体中一条晶棱方向上原子的排列，结构基元为相邻的一个Na+和一个Cl-；（b）为层型石墨分子中某些方向上碳原子周期排列的情况，２个Ｃ原子为一结构基元；（c）为伸展聚乙烯链的结构情况，结构基元为－CH2－CH2－。图中从各个结构基元抽象出点阵点，以黑点表示。由图可见，结构基元有时和化学组成的基本单位相同，而有时不同。

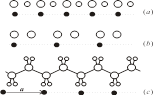
图7.1.1  一维周期排列的结构及其直线点阵（黑点代表点阵点）

（a）NaCl    (b)石墨    （c）伸展聚乙烯

直线点阵中相邻两个点阵点的矢量a是这直线点阵的单位矢量，矢量的长度a＝|a|，称为点阵参数，如图7.1.1（c）。直线点阵的代数表示可用平移群T=ma

（4）平面点阵  图7.1.2示出二维周期排列的结构及其平面点阵。图中：（a）为NaCl晶体内部一个截面上原子排列，其结构基元如虚线画出的正方形单位，包括一个Na+和一个Cl-，Cl-离子中心的黑点表示点阵点；（b）为层型石墨分子，其结构基元为２个C原子，如虚线划出的单位，每个结构基元以一个黑点表示。

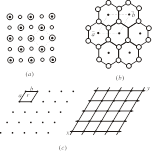
图7.1.2  二维周期排列的结构及其平面点阵（黑点代表点阵点）

（a）NaCl    (b)石墨    （c）平面点阵划分和平面格子

平面点阵必可划分为一组平行的直线点阵，并可选择两个不相平行的单位矢量a和ｂ划分成并置的平行四边形单位，点阵中各点阵点都位于平行四边形的顶点上。矢量a和ｂ的长度a＝|a|，b=|b|及其夹角g称为平面点阵参数，如图7.1.2（c）。其平移群为T=ma+nb。通过点阵点划分平行四边形的方式是多种多样的，虽然它们的点阵参数不同，但若它们都只含一个点阵点，它们的面积就一定相同。

（5）空间点阵  图7.1.3示出三维周期排列的结构及其空间点阵。图中：（a）为NaCl结构，一个Na+和一个Cl-构成一结构基元；（b）

为石墨结构，在这结构中,  4个C原子构成一结构基元。

空间点阵必可选择３个不相平行的单位矢量a，b，c，它们将点阵划分成并置的平行六面体单位，称为点阵单位。其平移群为Ｔm.n.p=ma+nb+pc。通常根据矢量a，b，c选择晶体的坐标轴x，y，z，使它们分别和矢量a，b，c平行。一般３个晶轴按右手定则关系安排：伸出右手的3个指头，食指代表ｘ轴，中指代表ｙ轴，大拇指代表ｚ轴。如图7.1.3（ｃ）所示者即为右手坐标轴系。

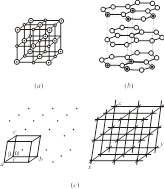
图7.1.3  三维周期排列的结构有其空间点阵（黑点代表点阵点）

（a）NaCl    (b)石墨    （c）空间点阵划分及晶格

（6）正当格子  对一个确定的平面点阵，平移向量a和ｂ可有多种选择方式。按选择的向量可将平面点阵点按平行四边形连成平面格子，每个平行四边形单位顶点位置的阵点为四个单位所公用，故对每个单位的贡献是1/4；边上的点阵点为两个单位公用，内部的点阵点为该单位独有。凡是分摊到一个阵点的单位称为素单位；分摊到两个或两个以上阵点的单位称为复单位。

平移向量a和ｂ选择的多样性决定了平面格子的形状和大小也是多样的。为了使研究问题方便，我们常选对称性高的含点阵点少的单位即正当单位，具体地说，选用的素向量间的夹角最好是90° ，其次是60°，再次是其它角度；选用的素向量尽量短。符合以上要求的平面正当格子只有四种形状五种型式，即正方形格子、矩形格子、矩形带心格子、六方格子和平行四边形格子（图7.1.4）。

 

图7.1.4  四种形状五种型式的正当格子

空间点阵按照确定的平行六面体单位连线划分，获得一套直线网格，称为空间格子或晶格。向量a、b、c的长度a、ｂ、ｃ及其相互间夹角ｂ∧c＝a、ｃ∧a＝β、a∧ｂ＝γ称为空间点阵的点阵参数。处于平行六面体顶点位置的阵点为８个单位所公用，对每个单位的贡献是1/8。按平行六面体分摊到阵点数是一个还是两个或两个以上可将空间格子分成素单位和复单位。按正当单位的要求，空间点阵的正当格子有七种形状十四种型式（详见下一个知识点）。

晶胞与晶胞二要素

（1）晶胞  空间点阵是晶体结构的数学抽象，对于实际的三维晶体，选择三个不相平行的、能满足周期性的单位向量a、b、c，可将晶体划分为一个个完全等同的平行六面体，它代表晶体结构的基本重复单位，叫做晶胞。整个晶体就是由晶胞按其周期性在三维空间重复排列而成的。

若一整块固体基本上为一个空间点阵所贯穿，称为单晶体。有些固体是由许多小的单晶体按不同的取向聚集而成，称为多晶，金属材料及许多粉状物质是由多晶体组成的。有些固体，例如炭黑，结构重复的周期性很少，只有几个到几十个周期，称为微晶。微晶是介于晶体和非晶物质之间的物质。

对于同一晶体，在划分平行六面体时，由于选择向量的方式（大小和方向）不同，当然有多种划分方法，也就能得到多种不同形状的晶胞。这些晶胞基本分为两类：素晶胞和复晶胞。素晶胞包含的内容实质上就是结构基元。图7.1.5和图7.1.6示出了两种晶体的不同晶胞的划分。图7.1.5中，若按素晶胞划分时,其对称性最高的单位只能是一个菱面体单位, 而按复晶胞划分时，则可得一个面上带心的立方体单位，显然立方体比菱面体对称性高，故这样的晶体必须按立方复晶胞划分。图7.1.6中，按素晶胞划分时, 其最高对称单位是一个（简单）四方体单位，按复晶胞划分时也是一个（底心）四方体单位，二者对称性相同，故必须按素晶胞（简单四方体单位）划分。

 

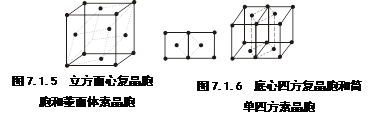
（2）晶胞的两个基本要素  晶胞是晶体结构的基本重复单位，因此，研究晶体结构只需搞清其晶胞即可。晶胞有两个基本要素：一个是晶胞的大小和形状，可用晶胞参数表示；另一个是晶胞中各原子的坐标位置，通常用分数坐标（x、y、z）表示。如图7.1.7所示，选择O点为晶胞的坐标原点，Ｐ点为晶胞中原子Ｐ的中心所在位置，该位置可用向量OP表示：OP＝xa+yb+zc，由于Ｐ点在晶胞内，x、y、z≤1，所以我们定义x、y、z为原子P的分数坐标。

图7.1.8是CsCl晶胞，而且是素晶胞，其中Cs+和Cl-的分数坐标分别为Cs+ (1/2 1/2 1/2)，Cl- (0 0 0)。

　　　　　　　　　　

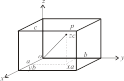
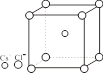
图7.1.7  分数坐标        图7.1.8  CsCl晶胞

由分数坐标和晶胞参数可计算出相邻原子间的距离（键长）。另外，对于同一晶体，由于晶胞的坐标原点选择不同，同一原子分数坐标的表示也不相同。因此，对一个晶胞来说，坐标原点选择应遵循一定的规律，一般在有对称中心的晶体中，原点选择在对称中心位置上。

晶面和晶面指标

（1）晶面   晶胞中坐标轴的确定不仅为研究原子位置提供了方便，也为解析晶体的晶面创造了条件。所谓晶面并非指晶体表面，也不是晶体或晶胞中任意划分出的一个平面，晶面是平面点阵所处的平面。如图7.１.9中，Ａ、Ｃ、Ｄ、Ｅ平面都是晶面，而Ｂ平面则不能称为晶面。

空间点阵可以从不同方向划分出不同的平面点阵组，每一组中的每个点阵平面都是互相平行的。各组平面点阵对应于实际晶体结构中不同方向的晶面，在这不同方向的晶面上，结构基元的排列情况是各不相同的，它们所表现的性质也就不同。为了区别这些不同的晶面，晶体学上引用了“晶面指标”（亦称晶面符号或密勒指标）这一概念。

　　　　　　　 

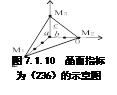
（2）晶面指标  晶面指标的严格定义是：晶面在三个晶轴上的倒易截数的互质整数之比。如图7.1.10所示，设一个晶面在三个晶轴上的截距分别是h¢a、k¢b和l¢c，由于三个晶轴的长度分别是以a、b、c为单位的，故将截距中的h¢、k¢、l¢分别叫做晶面在三个晶轴上的截数。它们的倒数1/h¢、1/k¢、1/l¢称做倒易截数。将这倒易截数之比化为一组互质的整数比h*:k*:l*, 即1/h¢：1/k¢：1/l¢＝h*:k*:l*可写为（h*k*l*）。此（h*k*l*）就是这个晶面的晶面指标。如图7.1.11即为（236）晶面。

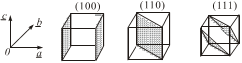
图7.1.11 立方晶体的几组晶面指标

很明显，用晶面指标标记晶面有其一定的方便之处：①由于采用了倒易截数，则避免了在晶面指标（h*k*l*）中出现¥。当一个晶面与某一晶轴平行时，可认为晶面在这个晶轴的截数为¥，而其倒易截数１/¥则为0，如图7.1.11所示。因此，若晶面指标中某一数为零，就意味着晶面与该指标对应的晶轴平行。②由于采用了互质整数比，所以一个晶面指标（h*k*l*）则代表一组平行晶面。只要是同一方向的晶面均可由一个（h*k*l*）表示。③晶面指标的数值也反映了这组晶面之间距离的大小及阵点的疏密。从图7.1.12中可以看出，晶面指标较小的平面点阵组（晶面），其面间距离较大，而且每个面上阵点的密度也较大。④由于晶面指标是由截长推求得到的，若知道一组晶面的指标（h*k*l*），则可求得这组晶面在三个晶轴上的截数与截长：

截  数	h¢=n/h*	k¢=n/k*	l¢=n/l*
截  长	110  h¢a	a  k¢b	l¢c

 

图7.1.12  平面点阵间距及阵点密度与晶面指标关系示意图

综合上述晶面和点阵间的相互对应关系，列于表7.1.1。

表7.1.1  点阵与晶体的相互关系

科学抽象的数学模型	空间点阵	(点)阵点	直线阵点	平面阵点	素单位	复单位
客观存在的实际结构	晶体	结构基元	晶棱	晶面	素晶胞	复晶胞

3.理想晶体与实际晶体中的缺陷

理想晶体与晶体缺陷  点阵理论所描述的晶体结构是理想的晶体结构，其中组成每一个结构基元的成分和结构都是完全相同的。这些结构基元在空间位置和取向上也完全规则的重复排列。但在实际晶体中，结构基元或其排列不可能是完美无缺的，会存在许多缺陷。

晶体中一切偏离理想的点阵结构都称为晶体缺陷。，如空位、杂原子置换、填隙原子的点缺陷（图7.1.13）；这些缺陷有的是晶体结构本身偏离点阵结构造成的，有的是外来杂质原子进入基质晶体所形成的。实际晶体内缺陷的存在会引起晶体点阵的畸变，缺陷和畸变存在的部位，由于正常的点阵结构受到一定程度的扰乱或破坏，对晶体一系列物理和化学性质都会产生影响，改变晶体缺陷的形式和数量，就可以制得所需性能的晶体材料。

 

图7.1.13  点缺陷示意图

a、空缺  b、置换  c、填隙