1.晶体的宏观对称性

晶体的宏观对称元素和对称操作  晶体的宏观对称性与有限分子的对称性一样也是点对称性，具有点群的性质，只有4种类型的对称操作和对称元素，如表7.2.1所列。

晶体的宏观对称性与有限分子的对称性最本质的区别是晶体的点阵结构使晶体的宏观对称性受到了限制。这种限制有两方面的含义：

①在晶体的空间点阵结构中，任何对称轴（包括旋转轴、反轴以及螺旋轴）都必与一组直线点阵平行，除一重轴外，

表7.2.1  晶体宏观对称性与分子对称性对照表

分子对称性		晶体宏观对称性
对称无素 及其符号	对称操作 及其符号	对称元素 及其符号	对称操作 及其符号
对称轴Cn	旋转n	旋转轴n	旋转L(a)
对称面s	反映	反映面或镜面m	反映M
对称中心i	反演	对称中心i	反演I
映轴Sn	旋转反映
		反轴	旋转反演L (a)I

任何对称轴还必与一组平面点阵垂直；任何对称面（包括镜面及滑移面）都必与一组平面点阵平行，而与一组直线点阵垂直。

②晶体中对称轴（包括旋转轴、反轴和螺旋轴）的轴次n并不是可以有任意多重，而是仅限于n=1、2、3、4、6。这一原理称为“晶体的对称性定律”。

准晶体  准晶体通过电子衍射能得到衍射斑点比较明锐的具有五次对称轴（如图7.2.1）或八次、十次、十二次对称轴等通常晶体不允许的衍射花样。

 

图7.2.1 五重对称的二十面体

准晶体的结构特征介于晶体和玻璃态非晶体之间，它不具备完全的周期性，但可能具有准周期性，没有平移点阵性质。

2.晶体宏观对称性的分类

宏观对称元素的组合和32个点群  晶体中可以只存在一个宏观对称元素，也可能有两个以上元素按一定方式组合起来而共同存在。对于宏观对称元素而言，进行组合是必须严格遵从两个条件的限制：第一，晶体的多面体外形是一种有限图形；第二，晶体具有周期性的点阵结构。只有不违背这两个限制条件的对称元素组合，才是合理的、可以容许的组合。

按照组合程序及其规律进行合理组合，不遗漏也不重复，可得到的对称元素系共32种，即32个点群。

表7.2.2中列出了32个点群包含的对称元素、一般常用的熊夫里斯符号和通用的国际记号。点群的国际符号是按照一定顺序排列的数字和字母，这种排列的先后顺序叫“位序”，大多记三位，表示晶体中三个方向的对称性。各个晶系在三个位置上规定的方向列于表7.2.3。

表7.2.2.  7个晶系的划分和32晶体学点群

对称性的高 低	晶     系	特征对     称元素	晶胞类型	点    群			对称元素①
				序号	熊夫里 斯记号	国际记号
低	三 斜	无	a¹b¹c	1	C1	1	—
			a¹b¹g¹90°	2	Ci		i
	单 斜	2或m	a¹b¹c	3	C2	2
				4	Cs	m	m
			a＝g＝90°¹b	5	C2h		，m，i
	正 交	二个互相垂直的m或三个互相垂直的2	a¹b¹c	6	D2	2 2 2	3
				7	C2v	mm2	，2m
			a＝b＝g＝90°	8	D2h		3 , 3 m, i
中	四     方	4	a=b¹c	9	C4	4
			a＝b＝g＝90°	10	S4
				11	C4h		，m，i
				12	D4	4 2 2	, 4
				13	C4v	4 m m	，4 m

				14	D2d	2m	，2 ，2 m
				15	D4h		，4 ，5 m，i
			菱面体晶胞	16	C3	3
	三 方	3	a＝b＝c	17	C3i		，i
			a＝b＝g<120° ¹90°	18	D3	3 2	，3
			六方晶胞	19	C3v	3 m	，3 m
			a＝b¹c a＝b＝g<120°¹90°	20	D3d		, 3 , , 3m，i
	六       方			21	C6	6
				22	C3h		(，m)
				23	D6h		，m，i
		6	a＝b¹c	24	D6	6 2 2	，6
			a＝b＝90°	25	C6v	6 m m	，6 m
			g＝120°	26	D3h	m 2	（，m）， 3 ，4m
				27	D6h		, 6 ，7m，i
高	立     方	43在立方体的体对角线方向	a＝b＝c a＝b＝g＝90°	28	T	2 3	4 , 3
				29	Th		4 ，3 ，3m，i
				30	O	4 3 2	4 ，3 ，6
				31	Td	3 m	4 ，3 ,，6m.
				32	On		4 ，3 ,，6, 9m, i.

①对称元素符号前的数字代表对称元素的数目，未注数字的表示为1。

表7.2.3  国际记号中位序相应的方向

对照“位序”分析国际符号，可知在这种晶胞中，在与a平行的方向上有4，与a垂直的方向有镜面m，在与a+b+c（体对角线）平行的方向有3，在与a+b（面对角线）平行的方向有2，与面对角线垂直的方向还有镜面m。

特征对称元素与7个晶系  在32晶体学点群中，可以发现某几个点群均含有一种相同的对称元素（一般指尽可能高次的对称轴），如T、Th、Td、O和Oh五个点群都有4个3，这样的对称元素称作特征对称元素。根据特征对称元素及数目的不同，可将32点群分为7类，正好对应于7类不同形状的晶胞，亦即7个晶系，见表7.2.2和图7.2.2。

 

 

图7.2.2  七个晶系和十四种空间点阵型式

分析表7.2.3可以发现，在每个晶系包含的几个点群中，含有对称中心i的那个点群，其对称性在该晶系中是最高的，可为这个晶系的代表。

明确了晶体对称性与晶胞规则性的关系，我们就可以根据晶体宏观外形的特征对称元素来判定晶体属于何种晶系，即按表7.2.2中由上而下的顺序，先找寻有无4个3，判断是否属于立方晶系；而后再考虑是否属于六方、四方等晶系，依此类推进行之。

十四种空间点阵  按正当格子的要求，空间正当格子只有七种形状（对应于七个晶系）十四种型式。图7.2.2中绘出了十四种空间点阵型式的具体形状。由于这些型式是由布拉维在1885年推引得出的，故也称为“布拉维空间格子”。

立方晶系不存在立方晶系的特征对称元素4个3；四方晶系只有P、I两种点阵型式，因为四方面心可由四方体心代替（图7.2.3），四方底心可由四方简单点阵来代替；正交晶系四种型式P、I、F、C（或侧心A或B）都有；单斜晶系有P、C两种型式；三方、六方、三斜都只有素格子，它们的点阵型式可分别用记号R、H、P来标记。

 

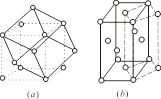
图7.2.3  (a)立方体心复单位和菱面体素单位

(b)四方面心复单位和四方体心复单位

3.晶体的微观对称性

晶体的微观对称元素和对称操作  晶体的微观对称性就是晶体内部点阵结构的对称性。一方面，由于晶体外型的对称性是其内部点阵结构（微观）对称性的宏观表现，所以晶体所有的宏观对称元素也应该是晶体的微观对称元素。另一方面，与有限的晶体外形不同，空间点阵是无限图形，存在平移这样的空间对称操作，因此晶体微观上还存在与空间对称操作相应的一些对称元素。所以，晶体的点阵结构使晶体的微观结构对称性在宏观对称元素的基础上还增加了下述三种类型。

（1）点阵（t）——平移操作（T）：点阵是晶体微观结构中最基本、最普遍的对称元素，这一对称性质，反映出了晶体结构的根本特征——周期性。与点阵相应的对称操作是平移（T）。

（2）螺旋轴（ni）——螺旋旋转操作：是由旋转与平移组成的一种复合对称操作。操作进行时，先绕轴旋转L（2p/n），而后再沿轴向平移T（ia/n），当然也可先平移再旋转，从而得到ni螺旋轴

ni=L（2p/n）·T（ia/n）

式中n=1，2，3，4，6；i=1，2，3，…，n。如图7.2.6，表示了点阵结构所具有的31螺旋轴。微观的螺旋轴与宏观的对称轴有一定的对应关系，若晶体宏观上有n，则微观上在与n平行的方向必有ｎi的一种或几种；反之亦然。

（3）滑移面——滑移反映操作：是由反映与平移组成的复合对称操作。如图7.2.5所示，根据滑移方向的不同，可分为三类。

轴线滑移面a（或b，或c）：为图7.2.5（a）所示的虚线位置，对应的操作为反映后再沿a（或b，或c）轴方向平移a/2（或b/2，或c/2）；

 

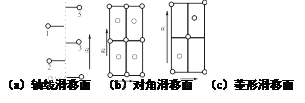
图7.2.4  31螺旋轴   图7.2.5  滑移面

对角线滑移面n：在图7.2.5（b）中，n位于纸面上，○和分别在纸面的上面且和下面与纸面的距离相等处。对应的操作是反映后沿a轴方向移动a/2，再沿b轴方向移动b/2，即反映后又平移a/2+b/2（a/2+c/2，b/2+c/2，a/2+b/2+c/2）；

菱形滑移面d（又称金钢石滑移面）：在图7.2.5（c）中，d也在纸面上，○和意义同上，对应的操作是反映后再平移a/4+b/4（或a/4+c/4，或b/4+c/4）。

上述滑移操作也可以先平移再反映。

 晶体的微观对称类型与230个空间群  如前所述，晶体的微观对称性是晶体点阵结构的对称性，它与宏观对称性的根本差别是

在宏观对称操作的基础上增加了点阵结构特有的平移操作，从而使晶体的微观对称性不再具有点对称性质。将晶体的微观对称元素进行组合时，不同的组合情况不要遗漏，也不要重复，可得到230种不同的微观对称元素系列，与这些微观对称元素系列对应的230个空间群（见附表）也就是晶体可能具有的微观对称类型（即可能有的空间点阵结构类型）。

表示空间群的国际符号与点群的国际符号相似，只是在序位之前增加了点阵型式。基于230个空间群是在32点群的基础上增加了平移操作而派生出的，故而属于同一点群的各种晶体可以隶属于若干个空间群。如点群为C2h-2/m的各种晶体可分属下列6个不同的空间群。

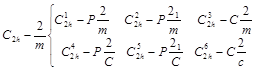
空间群在具体测定晶体结构，或从测得的晶体结构区分不同的晶体物质方面有着重要的意义，它是X射线晶体结构分析的基础。