1.X射线在晶体中的衍射

X射线是波长约50—250pm的一种电磁幅射，这个波长范围正好与晶体中的点阵面的间距大致相当，因此，可以用晶体作为X射线天然的衍射光栅。当用单色X射线照射晶体时，晶体中组成结构基元的原子周围的电子，受X射线周期变化的电场作用而振动，从而使每个电子（也可以说是整个原子）都变为发射球面电磁波的次生波源，形成次生X射线。由于是次生波源，所发射的球面波的频率、位相均与入射的X射线相一致，但又因为由平面波变成了球面波，故其传播方向部分发生了改变，这样的现象叫散射。散射引起的波与波之间的加强或削弱作用叫波的相干，故将上述散射称作相干散射。

并将次生X射线之间波的加强叫衍射。

X射线与晶体的相互作用如下:

 

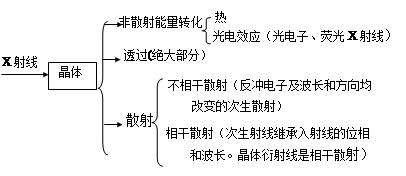
2.衍射方向与晶胞参数

晶体衍射方向是指晶体在入射X射线照射下产生的衍射线偏离入射线的角度。衍射方向决定于晶体内部结构周期重复的方式和晶体安置的方位。测定晶体的衍射方向，可以求得晶胞的大小和形状。

Laue方程  设有一直线点阵和晶胞的单位矢量a平行。S0和S分别代表入射X射线和衍射X射线的单位矢量，如图7.3.1所示。

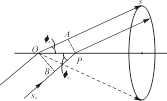
图7.3.1  Laue 方程的推导

若要求由每个点阵点所代表的结构基元间散射的次生X射线互相叠加，则要求相邻点阵点的光程差为波长的整数倍。这样，衍射方向单位矢量S和入射方向单位矢量S0与晶胞单位矢量a(即OP )间联系的方程为

光程差＝OA－BP＝a × s－a × s0＝hl            (7.3.1)

式中h为整数。若用三角函数表达，则为

a (cosfa－cosfa0)＝hl                (7.3.1¢)

(7.3.1)和(7.3.1¢)式称为Laue方程，它规定了当a和s0的夹角为fa0时，在和a呈fa角的方向上产生衍射，实际上以a作为轴线，和a呈fa角的圆锥面（劳埃圆锥）的各个方向均满足这一条件，如图中虚线所示。

将(7.3.1)或(7.3.1¢)式推广应用于晶胞的单位矢量b和c，可得相同的方程式。同时满足a, b, c和衍射矢量s的Laue方程组为

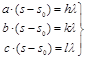                             (7.3.2)

或

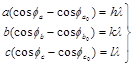                     (7.3.2¢)

（7.3.2）和（7.3.2¢）式中h, k, l均为整数，这组整数hkl称为衍射指标。晶体的衍射方向由s规定，从图形来看，s的方向为围绕a, b, c三轴线的圆锥面的交线方向。

衍射指标hkl的整数性决定了衍射方向的分立性，即只在空间某些方向上出现衍射。在这些方向上各点阵点之间入射线和衍射线的波程差必定是波长的整数倍。这结论可证明如下：从点阵原点000到点阵点mnp间的矢量为

Tmnp = mn+nb+pc

通过这两个点阵点的光程差D为

D = Tmnp ×(s-s0)

= ma×(s-s0)+nb×(s-s0)+pc×(s-s0)

= mhl+nkl+pll

= (mh+nk+pl)l

因m, n, p和h, k, l均为整数，故D必为波长的整数倍，这样满足(7.3.2)式的方向所有晶胞散射的次生射线都是互相加强的，这些方向就是衍射方向。

布拉格（Bragg）方程  若将空间点阵看成由互相平行且间距相等的一系列平面点阵(h* k* l*)所组成，则可得布拉格方程。

衍射指标(hkl)是一组任意整数，而晶面指标(h* k* l*)则是一组互质的整数。二者之间存在h＝nh*、k＝nk*、l＝nl*的关系。将空间点阵划分为平面点阵组时，在二相邻平面上任意各取一个阵点，该二阵点构成一直线点阵，并为相邻阵点，如图7.3.2，故其衍射线的光程差⊿也一定是波长l的整数倍。

 

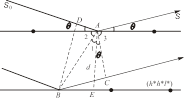
图7.3.2  (h* k* l*)平面点阵组的反射

在图7.3.2中，S0和S分别是X射线在入射方向和衍射（反射）方向的单位向量，与(h* k* l*)平面点阵组所成半衍射角为q nh* nk* nl*（以下证明过程为了书写方便，简写为q）；阵点A和阵点B是(h* k* l*)平面点阵组中晶面间距为（简写为d）二相邻平面上各任意选取的一个阵点，与二阵点组成了直线点阵。由图可知

AE＝  ⊿＝BC－AD＝nl  ÐCAE＝q

在直角三角形ABD中   AB＝AD/cos(Ð2+q)                (7.3.4)

在直角三角形ABC中   AB＝BC/sin(Ð1+q)                 (7.3.5)

在直角三角形ABE中   AB＝/cosÐ1                  (7.3.6)

可得  BC＝     AD＝

所以 ⊿＝BC－AD＝[sin(Ð1+q)－cos(Ð2+q)]        (7.3.7)

因为  Ð1+Ð2＝90°，所以  cosÐ2＝sinÐ1, sinÐ2＝cosÐ1

代入(7.3.7)式得  ⊿＝×2sinq

即        2sinq nh*nk*nl*＝nl                      (7.3.8)

此即布拉格方程。在该方程中，半衍射角q nh* nk* nl*＝qhkl，又叫布拉格角；整数n即为衍射级数，可取1, 2, 3, …整数。

布拉格方程中的晶面间距实际也是晶体中某一方向的直线点阵的周期，它与我们所需要的正当晶胞的晶胞参数有一定关系。因此，布拉格方程与劳埃方程一样，都是联系衍射方向和晶胞参数的重要方程。

用衍射指标hkl代替晶面指标，可以计算衍射面间距。例如立方晶系＝a/(h2+k2+l2)1/2，从而可得到立方晶系的布拉格方程为

sin2q＝(l/2a)2(h2+k2+l2)                        (7.3.9)

3.系统消光条件

晶体结构中如果存在着带心的点阵（或滑移面、螺旋轴）时，晶体结构按劳埃方程或布拉格方程原应该产生的部分衍射会成群地或系统地消失，这种现象叫系统消光。系统消光与晶体的点阵型式有关。现将部分点阵型式的系统消光条件列于表7.3.1。

表7.3.1  点阵型式与系统消光条件

点阵形式	消光条件
体心点阵（I）	h+k+l=奇数
面心点阵（F）	h、k、l奇偶混杂
底心点阵（C）	h+k=奇数
A面侧心点阵（A）	k+l=奇数
B面侧心点阵（B）	h+l=奇数
简单点阵（P）	无消光现象
·0作为偶数