晶体的结构取决于晶体中原子或基团的空间结构及其堆积型式，同时，与其内部的电子运动状态密切相关。晶体的周期性结构使其电子运动状态受到重要影响，随着分子结构的有规则延伸和扩张，能级增多、密集，逐渐转变为能带，分子轨道成为晶体轨道。即将单电子模型用于晶体，形成了晶体的能带理论。

一、晶体结构的能带理论

1.能带及其类型  以k为横坐标，E (k)为纵坐标，画出能带曲线。图8.1.1描述了能带结构曲线。

 

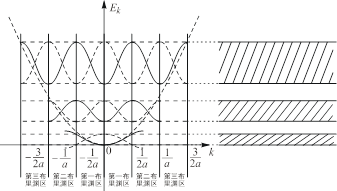
图8.1.1  能带的形成

以金属锂晶体为例，如图8.1.2所示。由于孤立锂原子的1s与2s能量相差很大，所以锂晶体的1s能带与2s能带之间也有很大的间隔，即为禁带；又因1s轨道是填满电子的，故1s能带也是填满的称为满带；2s轨道中仅有一个电子，故2s能带中仅能量较低的那一半能级上填有电子，这种未被电子完全填满的能带称为导带；2p能带是全空的称为空带；因为孤立Li原子的2s与2p轨道能量相差不大，结果2s能带与2p能带部分重叠，称为叠带或重带。叠带也有满带、导带和空带之分。

 

图8.1.2  锂的能带示意图

在上述能带中凡是填有价电子的能带称为价带。价带和与其毗邻的空带以及两者之间的禁带是晶体能带中最重要的部分。价带中电子的填充情况（满或缺）决定了该晶体中电子的活跃程度，是晶体能否导电的根本原因。禁带的大小不仅决定价带与空带间电子跃迁的难易，而且也影响到晶体中成键的强弱。价带以下的内层的能带皆为满带。它们一般对晶体的成键没有贡献，又因不毗邻空带，不可能发生能带之间的电子跃迁。

二、晶体结构的密堆积原理

1. 等径圆球的堆积

如图8.1.4所示。在层中每个球和周围6个球接触，即配位数为6。在密堆积层中，每个球周围有6个空隙，每个空隙由3个球围成，这样由N个球堆积成的层中，有2 N个空隙，平均每个球摊到2个空隙。

 

8.1.4  密堆积层的结构

图中A表示球心的位置，B表示顶点向上的三角形空隙（D）

的中心位置，C表示顶点向下的三角形空隙（Ñ）的中心位置。

（1）常见的两种最密堆积的结构

①立方最密堆积。将密堆积层的相对位置按照ABCABCABC…方式作最密堆积，这时重复的周期为3层，如图8.1.5（a）。由于这种方式可划出面心立方晶胞，如图8.1.5（b）,故称为立方最密堆积，记为A1型。

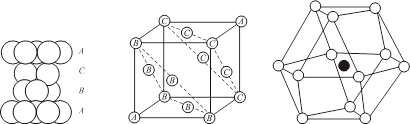
（a）堆积图示     （b）面心立方晶胞      （c）配位情况

8.1.5  A1型最密堆积及其晶胞

②六方最密堆积。将密堆积层的相对位置按照ABABAB…方式作最密堆积，这时重复的周期为两层，如图8.1.6(a)。由于这种方式可划出六方晶胞，如图8.1.6 (b)，故称为六方最密堆积，记为A3型。

在等径圆球最密堆积的各种形式中，每个球的配位数均为12，中心的球和这12个球的距离相等，这12个球的配位形式有所不同，图8.1.6与8.1.7中示出典型的两种情况：立方最密堆积配位（c）和六方最密堆积配位（c）。

 

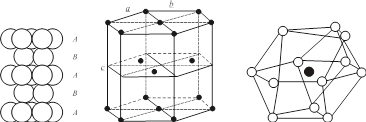
（a）堆积图示     （b）六方晶胞     （c）配位情况

8.1.6 A3型最密堆积及其晶胞

等径圆球的各种最密堆积形式均具有相同的堆积密度，其堆积系数即球体积与整个堆积体积之比（也叫空间利用率）均为0.7405。在各种最密堆积中，球间的空隙数目和大小也相同。由N个半径为R的球组成的堆积中，平均有2 N个四面体空隙，可容纳半径为0.225 R的小球；还有N个八面体空隙，可容纳半径为0.414 R的球。

在立方最密堆积和六方最密堆积中，八面体空隙和四面体空隙的分布情况示于图8.1.7（a）和（b）中。

 

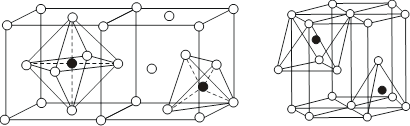
（a）A1密堆积中的空隙        （b）A3密堆积中的空隙

8.1.7 最密堆积中的空隙

（2）体心立方密堆积（A2）和金刚石型堆积（A4）

①体心立方密堆积（A2）。 A2密堆积不是最密堆积。其结构如图8.1.8所示，每个圆球均有8个最近的配位圆球，处在边长为a的立方体的8个顶点处，距离为d＝a/2；另外还有6个稍远些的配位圆球，分别处于和这个立方晶胞相邻（前后左右上下）的六个立方体中心，故其配位数也可看作14。堆积系数为68.02%。

 

（a）体心立方晶胞     （b）堆积情况     （c）配位情况

8.1.8  体心立方密堆积及其晶胞

在体心立方结构中，存在由6个圆球围成的八面体空隙，空隙的中心处在晶胞的每个面心处和每条边的中心点上，如图8.1.9所示。这种八面体空隙不是正八面体形状，而是沿着一个轴压扁的八面体空隙，空隙中可容纳小球的半径r与堆积圆球的半径R之比为r/R＝0.154。另一种空隙为变型的四面体空隙，中心处在晶胞的面上，每个面有4个四面体中心。这种空隙的r/R＝0.291。

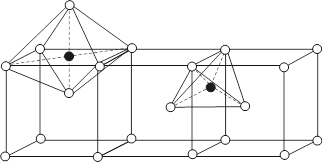
8.1.9 体心立方堆积中的空隙

②金刚石（四面体）型堆积（A4）。 这种配位数为4的堆积，堆积密度较低，堆积系数只有34.01%，不是密堆积。

总结上述各种堆积型式，汇总数据于表8.1.1。

表8.1.1  几种主要堆积型式的数据

堆 积 名 称	记号	堆积系数	配位数	空 隙 大 小		实例
				八 面 体	四 面 体
立方最密堆积	A1	71.05	12	r＝0.414R	r＝0.225R	Cu
六方最密堆积	A3	71.05	12	r＝0.414R	r＝0.225R	Mg
体心立方密堆积	A2	68.02	8(或14)	r＝0.154R	r＝0.291R	K
金刚石型堆积	A4	34.01	4		R＝0.433a	Sn，Ge
注：表中R为堆积圆球的半径，r为填隙小球的半径，a为立方晶胞的边长。

组成晶体的微粒的堆积型式及其空隙的数目、大小和形状以及分布特征，直接影响到晶体的结构性质，因而密堆积原理是晶体结构的普遍原理。

2、密堆积原理的应用示例

（1）堆积系数（空间利用率）的求算  在A4型堆积中，如图8.1.10，设晶胞边长为a，则该立方体晶胞的体对角线l＝a；设＝d，则d为A 4型堆积中一个正四面体的中心圆球心到配位圆球心的距离。那么，密集等径圆球的半径自然应该为该距离的一半，即R＝。由于O点和P点的分数坐标分别为O (0, 0, 0)和P ()，所以

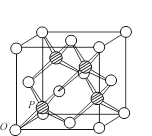
8.1.10  四面体型晶胞       

 

由此可知，在金刚石型堆积中，密集等径圆球的半径R应为晶胞边长a的倍。又因为A4型单位晶胞共含有半径为的圆球

n＝8×1/8+6×1/2+4×1＝8（个）

故而A4型堆积的堆积系数为

＝＝34.01%

同理可求得A1、A3和A2型的堆积系数。

堆积系数越大的堆积结构越稳定。所以绝大多数金属晶体、合金晶体、分子晶体等都采用最密堆积结构。

不等径球的填隙堆积  为了获得稳定的结构，不等径球的堆积基本上都可以以大球的最密堆积结构了解其特征，而小球根据半径的不同全部或部分的填充于八面体或四面体空隙之中，如图8.1.11所示。这种填隙堆积结构，堆积系数更大。

 

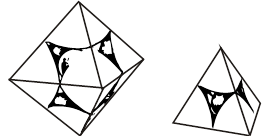
（a）           （b）

8.1.11  填隙八面体（a）和填隙四面体（b）