一、离子晶体的典型结构型式和离子键

1.离子晶体的典型结构形式 

几种典型离子晶体的结构型式简释于表8.3.1，并示于图8.3.1。

表8.3.1  典型离子晶体的结构

典型离子晶体	点阵	结构基元数	配位数比	填隙的类型和分数	堆积型式
NaCl	立方F	4个NaCl	6:6	全部八面体空隙	ccp
CsCl	立方P	1个CsCl	8:8	全部立方体空隙	简单立方
立方ZnS	立方F	4个ZnS	4:4	1/2四面体空隙	ccp
六方ZnS	六方H	2个ZnS	4:4	1/2四面体空隙	hcp
NiAs	六方H	2个NiAs	6:6	全部八面体空隙	hcp
CaF2	立方F	4个CaF2	8:4	全部四面体空隙	ccp
金红石	四方P	2个TiO2	6:3	1/2八面体空隙	hcp

 

 

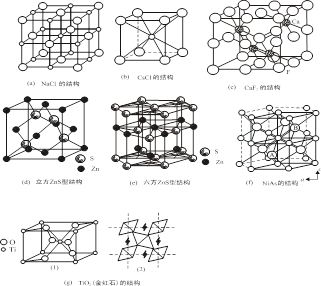
图8.3.1  典型离子晶体的结构

2.离子键的本质 

离子化合物中，正、负离子之间通过库仑作用结合在一起，这种化学键称为离子键。离子键源于离子间的静电相互作用，没有方向性和饱和性。离子键向空间各方向发展，即形成离子晶体。

值得注意的是，离子键实质上是共价键中极性键的极限情况。在实际晶体中，单纯的离子键很少，甚至那些很熟悉的离子化合物，共价键作用也非常重要，而且往往是几种键型兼而有之，故而能带理论也适用于离子晶体。离子晶体的能带结构可以由原子轨道推引得到。例如，NaCl晶体是由Na+和Cl-组成，它们具有由Cl-的3p能级组成的满带和由Na+的空的3s能级组成的空带，由于是两种不同原子的3s和3p能级，能量相差很大，故其禁带较宽，

不可能重叠，电子很难激发跃迁，所以NaCl晶体是绝缘体。

由于离子晶体结构的特殊性，形成了离子键理论，其主要内容包括离子晶体的点阵能、离子极化和键型变异现象、以及离子半径等。

二、点阵能的计算

1.点阵能  离子键的强弱可用点阵能的大小来表示。点阵能又叫晶格能，指在0 K时，1mol离子化合物的正、负离子由相互分离的气态结合成离子晶体时所放出的能量。若用化学反应式表示，点阵能相当于下一反应的内能改变量

点阵能越大，表示离子键越强，晶体越稳定。

2.点阵能的计算  从离子晶体的特点出发，玻恩等假设离子晶体中的作用力主要是库仑（Coulomb）力，并根据库仑定律，从理论上导出了计算点阵能的公式。对于NaCl型离子晶体

其点阵能为

               （8.3.1）

对于MyXx晶体

其点阵能为

                   （8.3.2）

8.3.1和8.3.2式中，R0为紧邻正、负离子间的平衡距离；NA为阿伏加德罗常数；e为电子电荷；z+、z－分别为正、负离子所带的电荷；叫做玻恩指数，对碱金属卤化物m»9左右；r为一常数，对于碱金属卤化物r»0.031nm;a, a¢, a² 均称为马德隆（Madelung）常数，它与晶体结构的类型有关，在不同的晶体结构型式中，其值不同。

例如,用 X 射线结构分析测得 NaCl 晶体立方面心结构的晶胞参数 a

= 5. 628 pm,则 Na + 和 Cl - 的平衡距离即键长 R0 = a / 2 = 2. 814 pm,可得 NaCl

晶体的点阵能 U

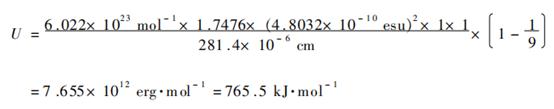
也可以利用玻恩–哈伯循环测定推求点阵能。

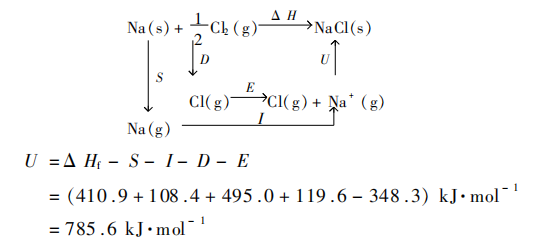
三、离子极化和键型变异现象

离子键、共价键和金属键只是三种极限键型，实际晶体中，少数是纯粹属于这三种键型之一，而多数晶体则往往偏离这三种典型的键型，使得几种键型兼而有之。因此，离子晶体结构的许多问题，也是和现代化学键的概念和原子轨道及分子轨道的成键作用、电子的离域效应、离子的极化等因素密切相关的，只要某种条件具备，就会产生和这种条件相应的成键作用。

1.离子的极化  卤化银（AgX）的结构可作为由离子键向共价键过渡的例证。分析AgX的组成和离子半径，均应为配位数为6的NaCl型结构，但AgI实际上却是配位数为4的ZnS型结构。这主要是由于离子的极化所致。

从已学过的离子极化的有关概念，根据静电理论，离子所带电荷越多，体积越小，产生的电场强度越大，其极化力也越大；一般地大致与w2/r（w为电价数，r为离子半径）成正比。另外，含有dn电子的离子，比一般离子的极化力强。离子的可极化性或变形性则取决于该离子的核对外层电子束缚的程度，以及外层电子的数目和排布方式。

此外，离子在外电场作用下，产生诱导偶极矩，其大小与电场强度E成正比。即

叫做诱导极化率，可简称为极化率。它等于离子在单位电场强度的电场作用下产生的诱导偶极矩。离子极化率的大小，是离子可极化性的量度。表8.3.4列出了一些离子的极化率和离子半径数值。由表列数据可总结出一些规律性：同价离子的半径越大，和与此相联系的负离子价数越高，正离子价数越低，极化率和可极化性越大。因此，正离子中的Cs+，负离子中的Br-、I-、S2- 等都具有较高的极化率和变形性。另外，含有dn电子的正离子（如含有d10电子的Ag +、Zn 2+、Cd 2+、Hg 2+等），比半径相近的其它正离子具有较大的极化率和变形性。

表8.3.4  离子的极化率

离子	极化率 a/Å3	半径 g/Å	离子	极化率 a/Å3	半径 g/Å	离子	极化率 a/Å3	半径 g/Å
Li+	0.031	0.60	Ba2+	1.55	1.35	Ce4+	0.73	1.01
Na+	0.179	0.95	B3+	0.003	0.20	F-	1.04	1.36
K+	0.83	1.33	Al3+	0.052	0.50	Cl-	3.66	1.81
Rb+	1.40	1.49	Sc3+	0.286	0.81	Br-	4.77	1.95
C5+	2.42	1.69	Y3+	0.55	0.93	I-	7.10	2.16
Be2+	0.008	0.31	La3+	1.04	1.04	O2-	3.88	1.40
Mg2+	0.094	0.65	C4+	0.0013	0.15	S2-	10.2	1.84
Ca2+	0.47	0.99	Si4+	0.0165	0.41	Se2-	10.5	1.98
Sr2+	0.86	1.33	Ti4+	0.185	0.68	Te2-	14.0	2.21

2.键型变异现象  离子的极化对晶体的键型和结构型式将产生影响。极化力强和变形性大的离子之间，特别是含dn电子的正离子（如Ag +、Zn 2+、Hg 2+等），与极化率大的负离子（如S 2-、I –、Br - 等）之间，产生较大的相互极化，导致离子键向共价键过渡，这种现象称为键型变异现象。相应地，也产生配位数降低的效应（如AgX中AgI晶体的配位数由6降低到4）。同时，随着键型和结构型式的变异，键长也相应地比离子键长的理论值（即离子半径和）逐渐缩短。这就又进一步使得键能和点阵能增大。由此也可解释卤化银中只有AgF可溶于水，而AgCl、AgBr和AgI的溶解度显著下降。因为随着键型中共价性成份的增多，在溶剂水作用下，将键拆开也越来越困难。同时也可明显地看出，如前面讲离子键的结构型式时所说的，ZnS晶体中的键是共价健而不是离子键。

在d轨道参加成键的条件下，有时会出现多种多样的键型，甚至有时很难确切说明是什么键。一种元素的原子在不同的化合物中，可以出现多种键型，甚至在一种化合物中，同种原子也有多种键型。

总之，在化合物中各个原子之间只要满足成键的条件，就可形成多种型式的化学键，通过这些成键作用，促使原子轨道互相有效地重叠，促进异号电荷间的吸引力加强，从而使分子和晶体的势能降低，稳定性增加。

3.晶体化学定律  哥希密特（Goldscmidt）对上述决定和影响离子晶体结构型式和配位数的因素做了简明扼要的规律性概括。他指出：“晶体的结构型式，取决于其结构基元（原子、离子或原子团）的数量关系、离子的大小关系和极化作用的性质。”这一概括叫做哥希密特晶体化学定律。此一定律不仅适用于离子晶体，也适用于其他晶体。晶体化学定律所指出的决定晶体结构的三个因素是一个整体，一般不应隔离开来看待。但在某些情况下，三者之中可能某一方面起主要作用，这要根据具体情况而定。晶体的类质同晶现象如CaCO3和NaNO3同晶体和同质多晶现象如立方面心ZnS和六方ZnS，亦可用晶体化学定律分析其成因。

四、离子半径

在离子晶体中，相邻的正、负离子间存在着静电吸引力和离子的外层电子云相互作用的排斥力。当这两种作用力达成平衡时，离子间保持一定的接触距离。排斥力是短距离性质的作用力，当正、负离子接近时，排斥力随距离的缩短而迅速增加。所以，离子可近似地看作具有一定半径的弹性球，两个互相接触的球形离子的半径之和等于核间的平衡距离，因此离子半径指离子在晶体中的“接触”半径。由原子结构可以了解电子在原子核外是连续分布的，并无明确的界限，离子半径的数值也是和离子所处的特定条件有关的。

1.离子半径的测定  利用X射线衍射法可以精确地测得正、负离子间的平衡距离。用其推求离子半径通常用两种方法：一种是从圆球堆积的几何关系来推算，所得结果称为哥希密特（Goldschmidt）半径；另一种是考虑到核对外层电子的吸引等因素计算离子半径，所得结果叫鲍林（Pauling）半径。

（1）哥希密特离子半径  以立方面心结构的NaCl型离子晶体为标准，从立方晶胞的一个面来看，如图8.3.2，可以有三种情况。若通过测定晶胞常数，能确定某离子晶体属于图中（a）的情况，由于便可计算r- ；在r-已知的情况下，再通过结构型式（c），可进而计算r+。

 

8.3.2  立方面心晶胞中正、负离子的接触情况

（a）负离子相互接触，正负离子不相接触；

（b）负离子之间及正负离子之间都相接触；

（c）正负离子之间相互接触，负离子之间不接触

还可看出，在三种氧化物中，至少MnO和CaO中的O 2-已被正离子撑开，而属于图8.3.2（c）的情形。而MgS和MnS的晶胞参数几乎相等，但<，说明MnS中的Mn2+还没有将S2-撑开；至少MgS属于图8.3.2（a）的情形，MnS则属于图8.3.2（a）或（b），即它们中的负离子与负离子接触。此时

在CaS晶体中，S2-已明显被Ca2+撑开，即正离子与负离子相接触。此时

CaO既属于图8.3.2（c），则利用上述算得的，又可求得。其它离子半径也可依此推算。如由表8.3.4中的数据，还可以推算，并证明MgO亦属于图8.3.2（c）的情况。

哥希密特按上述方法，并以测定值、为基准，确定了80多种离子的半径值，被称为哥希密特离子半径。至今仍在广泛使用。

（2）鲍林晶体半径  1927年Pauling根据5个晶体（NaF、KCl、RbBr、CsI和Li2O）的核间距离数据，用半经验方法推出大量的离子半径。因为离子的大小由它最外层电子的分布所决定，而最外层电子的分布与有效核电荷成反比，即

                  （8.3.3）

式中Cn为由量子数n决定的常数，对于等电子的离子或原子，Cn取相同数值。屏蔽常数可按Slater规则估算。

2.有效离子半径  Shannon（沙农）等归纳整理实验测定的上千个氧化物和氟化物中正负离子间距离的数据，并假定正负离子半径之和即等于离子间的距离，考虑了配位数、电子自旋状况、配位多面体的几何构型等对正负离子半径的影响，对某种固定的负离子、结构类型相同的一系列化合物，其晶胞体积正比于正离子的体积（但不一定是直线关系）。他们以 Pauling提出的配位数为6的O2 -半径为140pm，F -半径为133pm作为出发点，用Goldschmidt方法划分离子间距离为离子半径，经过多次修正，提出一套较完整的离子半径数据，称为有效离子半径。所谓“有效”，是指这些数据是由实验测定的数据推得，而离子半径之和与实验测定的离子间的距离相比，符合得最好。（若从O2-半径为132pm出发，可得另一套半径值。）

3.离子半径的变化规律

（1）周期表中离子半径的变化趋势有以下共同规律  ①同一周期核外电子数相同的正离子系列中，离子半径随正电荷数的增加而下降；②在s、p区，同族元素的离子半径从上到下逐渐增大；③周期表中左上方和右下方对角线上元素的相应价态离子，如Na+、Ca2+和Y3+；T i4+、Nb 5+和W6+等，其离子半径接近；④同一元素各种价态的离子，电子数越多，离子半径越大；⑤核外电子数相同的负离子对，如F -（133 pm）和O2-(140pm)，随着负电价的增加而半径略有增加；⑥镧系元素三价离了的半径（6配位），从La3+的103.2pm随着原子序数的增加逐渐下降到Lu3+的86.1pm。此为镧系收缩效应所引起，原子半径也有镧系收缩效应。由于镧系收缩，使得镧系后元素离子半径相应地也有所减小，以致锆与铪、铌和钽、钼和钨等同族的第五和第六周期元素具有大致相等的原子半径和离子半径。与镧系同族的Y3+的离子半径为90 pm，性质与镧系相似，故通称的稀土元素包括Y在内。

（2）正负离子半径比对离子晶体结构型式的影响  正、负离子半径的相对大小，直接影响到离子的堆积方式和离子晶体的结构型式。每个离子都力求与尽可能多的异号离子接触，以使体系的能量尽可能低。一般说来，负离子较大，正离子较小；离子的堆积，一般是负离子按一定方式堆积起来，而较小的正离子则嵌入到负离子之间的空隙中去。这样，一个正离子周围配位的负离子数（配位数），将受到正、负离子半径比r+/r1的限制。如图8.3.3，若三个负离子堆积成一个正三角形，在其空隙中嵌入一个正离子，恰与三个负离子相切，配位数为3。由图中的小三角形可知

所以

对于NaCl型晶体，若为图8.3.1（a），配位数为6. 不难计算得r+/r-= 0.414. 同样，可算得当负离子堆积成正四面体，其空隙处恰好嵌入一个正离子（配位数为4），则半径比r+/r-=0.225.

以上是正、负离子和负、负离子均接触的情况。若0.155<r+/r-<0.225，则正离子将会把如图8.3.3中的三个负离子撑开，但配位数仍保持为3，还不足以形成配位数为4的正四面体型；否则正、负离子不能接触。按此，可总结出离子半径比跟离子晶体中配位数的关系，如表8.3.4。根据这种关系，可解释为什么性质相似的离子化合物有不同的结构型式，也可根据离子半径的表值预测离子化合物的晶体结构型式。

表8.3.4  离子半径比与配位数的关系

	配位数	配位多面体构型
0.155 ~ 0.225	3	三角形
0.225 ~ 0.414	4	四面体
0.414 ~ 0.732	6	八面体(NaCl型)
0.732 ~ 1.000	8	立方体(CsCl型)
1.000	12	最密堆积