在力学、物理学以及日常生活中，会经常遇到许多种量，例如温度、时间、质量、密度、功、长度、面积与体积等，这些量在规定的单位下，其大小都可以由一个“数”来完全确定, 称这种只有大小的量为数量。另外还有一些较复杂的量，例如位移、力、速度、加速度等,它们不但有大小，而且还有方向，这种量就是矢量。

定义1  既有大小又有方向的量称为矢量，或称矢量，简称矢。

我们用有向线段来表示矢量，有向线段的起点与终点分别称为矢量的起点（或始点）与终点，有向线段的方向表示矢量的方向，而有向线段的长度表示矢量大小。起点为，终点为的矢量记作，有时也用,…或黑体字母,…来记矢量（图1-1）。矢量的大小称为矢量的模，也称矢量的长度。矢量与的模分别记做 与。

模等于1的矢量称为单位矢量，与矢量具有同一方向的单位矢量称为矢量的单位矢量，常用来表示。

模等于0的矢量称为零矢量，记作0，它是起点与终点重合的矢量，零矢量的方向不定（或称方向任意）。不是零矢量的矢量称为非零矢量。

由于在几何中，我们把矢量看成一个有向线段，下面提到的矢量与相互平行，即是指它们所在的直线相互平行，记做，类似地我们可以说一个矢量与一条直线或一个平面平行等等。

定义2 如果两个矢量的模相等且方向相同，则称它们为相等的矢量。规定所有的零矢量都相等。矢量与相等，记做。　

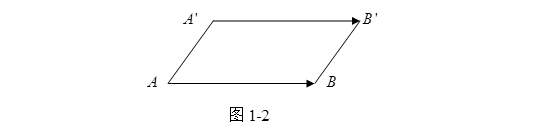
根据定义2，对于两个相等且不在同一直线上的非零向量与（图1-2），分别连结它们的一对起点与，一对终点与，则显然得到一个平行四边形，反之在平行四边形中，这样的一对矢量也必然模相等且方向相同即二矢量相等。

由于在很多情况下，矢量所描述的量只与该量的大小和方向有关而与矢量的起点无关，因此两个矢量是否相等只由它们的模和方向决定而与它们的起点无关，我们称这种只由模和方向决定的矢量为自由矢量。除非特别说明，在本课程中所讨论的都是自由矢量。

也就是说，自由矢量可以任意平行移动，移动后的矢量仍然是原来的矢量。 在自由矢量的定义下，相等的矢量都看作是同一个自由矢量，由于自由矢量始点的任意性，按研究的需要我们当然可以选取某一点作为一些矢量的公共起点。

必须注意，由于矢量不仅有大小，而且还有方向，因此，模相等的两个矢量不一定相等，因为它们的方向可能不同。

定义3  两个模相等，方向相反的矢量互称为反矢量（或负矢量），矢量的反矢量记做。

显然，矢量与互为反矢量，也就是, 或。如果把彼此平行的一组矢量归结到共同的始点，这组矢量一定在同一条直线上；同样，如果把平行于同一平面的一组向量归结到共同的始点，这组矢量一定在同一个平面上。

定义4  平行于同一直线的一组矢量，称为共线矢量。零矢量与任何共线的矢量组共线。

定义5  平行于同一平面的一组矢量，称为共面矢量。零矢量与任何共面的矢量共面。

显然，一组共线矢量一定是共面矢量，三矢量中如果有两矢量是共线的，这三矢量一定也是共面的。