在空间任意取定点，从引出三个不共面的矢量,那么空间任何矢量都可以分解成的线性组合

 ,               (1)

并且这里的是唯一的一组有序实数。

定义1空间中的一个定点，连同三个不共面的有序矢量的全体，称为空间的一个标架，记做。 若都是单位矢量，则 称为笛卡儿标架；若都是单位矢量，且两两相互垂直，则称为笛卡儿直角标架，简称直角标架；在一般的情况下，称为仿射标架。

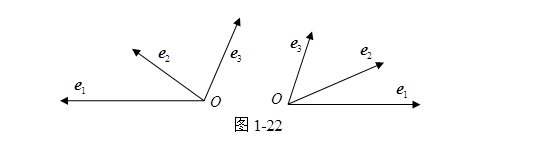
对于标架，如果的相互关系和右手拇指、食指、中指相同，那么这个标架称为右旋标架或右手标架。如果的相互关系和左手拇指、食指、中指相同，那么这个标架称为左旋标架或左手标架。（图1-22）

定义2 称（1）式中的为矢量关于标架的分量或称为坐标，记做或。

定义3  空间中取定标架，对于空间中任意点，矢量称为点的矢径，矢径关于标架的分量称为点关于标架的坐标，记做 或。

当空间取定标架之后，空间全体矢量的集合或者全体点的集合与全体有序三数组的集合具有一一对应的关系，这种一一对应的关系称为空间矢量或点的一个坐标系。

由于空间坐标系由标架完全决定，因此空间坐标系也常用标架来表示，这时点称为坐标原点；矢量都称为坐标矢量。

由右旋标架决定的坐标系称为右旋坐标系或称右手坐标系, 由左旋标架决定的坐标系称为左旋坐标系或称左手坐标系;仿射标架、笛卡尔标架与直角标架所确定的坐标系分别称为仿射坐标系、笛卡尔坐标系与直角坐标系。

我们特别约定,以后用到直角坐标系时,坐标矢量用表示,即用表示直角坐标系,我们以后在讨论空间问题时,所采用的坐标系,一般都是空间右手直角坐标系。

过点沿着三坐标矢量的方向引三轴, 这样我们也可以用这三条具有公共点的不共面的轴与来表示空间坐标系,并把它记做, 这时点 称为空间坐标系的坐标原点，三条轴与都称为坐标轴，并依次称为轴,轴与轴。每两条坐标轴所决定的平面称为坐标面，按照坐标面所包含的坐标轴, 分别称为平面,平面与平面。

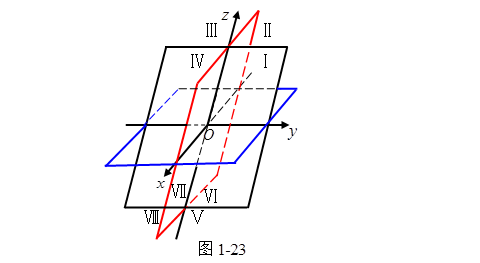
三个坐标平面把空间划分成八个区域,每一个区域都称为卦限，如图1-23中的八个区域，按排列顺序, 依次称为第卦限, 第卦限,… ,第卦限。

显然在坐标面上的点的坐标有一为零,例如面上的点的坐标 中。在坐标轴上的点的坐标有两个为零,例如轴上的点的坐标中,原点的坐标为。

在同一卦限内点的坐标的符号是一致的,但不同卦限内的点的坐标符号就不一样。各卦限内点的坐标的符号如下表所示：

类似地,利用矢量可以引进平面上的标架与坐标的概念。在平面上取定点与两不共线的矢量，那么它们就构成了平面上的标架,可以把平面上的任意矢量与有序实数对之间建立一一对应关系，而平面上的任意点，通过径矢也可与有序实数对建立一一对应，这样由标架就确定了平面上的一个坐标系，并记做，而矢量与点的坐标分别记做与。

过点沿与的方向分别引两轴。这就是坐标轴，为坐标原点，我们也可以用来记平面坐标系。如果都是都是单位矢量，且垂直于，那么这时所确定的坐标系，就是我们所熟知的平面直角坐标系。在一般情况下，我们称它为平面仿射坐标系，我们约定，平面直角坐标系的坐标矢量改为单位矢量, 并用来记平面直角坐标系。

下面我们用坐标进行矢量的运算。  

1)  用矢量的始点和终点的坐标表示矢量的分量

定理1  矢量的分量等于其终点的坐标减去其始点的坐标。

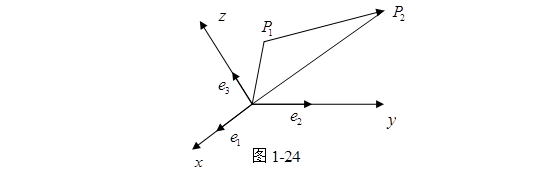
证  设矢量的始点与终点分别为与（图1-24），那么

 ,

,

所以 

 

,

即

      (1.5−1)

2)  用矢量的分量进行矢量的线性运算

定理2  两矢量和的分量等于两矢量对应的分量的和。

证  设, (图1-24)，那么

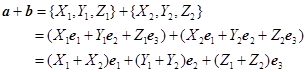
所以

      (1.5−2)

定理3   数乘矢量的分量等于这个数与矢量的对应分量的积。

证  设, 那么

所以

             (1.5−3)

3)  两矢量共线的条件,三矢量共面的条件

定理4 两个非零矢量 , 共线的充要条件是对应分量成比例,即

.             (1.5−4)

证  非零矢量共线的充要条件是其中一矢量可用另一矢量来线性表示, 不妨设, 于是

,

由此得到     

 , 

所以

当分母为零时,我们约定分子也为零。

推论1  三个点和共线的充要条件是

       (1.5−5)

定理5   三个非零矢量, , 共面的充要条件是

           (1.5−6)

证  非零的三个矢量共面的充要条件是存在不全为0的数使得

,

由此可得

,

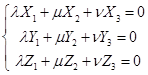因为不全为零，所以

.

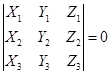推论2  四个点共面的充分必要条件是

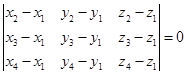        (1.5−7) 

或

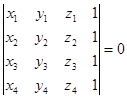.            (1.5− 7′)

4) 线段的定比分点坐标.

对于有向线段, 如果点满足，我们就称点是把有向线段分成定比的分点。根据上述条件，给定了点, 分点就由唯一确定。当时，和同向，点是线段内部的点；当时，和反向，是线段外部的点。并且注意，, 不然，如果, 将有 由此得，故, 与条件 矛盾。

定理6 有向线段的始点为, 终点为（图1-25） ， 那么分有向线段成定比的分点P的坐标是

.         (1.5−8)

证  由已知条件得   ,

而          ，,

　

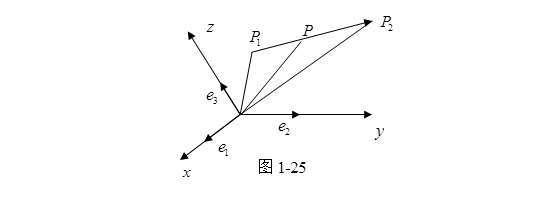
所以 

,

从而有         将的分量代入，得点的坐标为

 .

推论3  设, 那么线段的中点坐标是    

 .        (1.5−9)

例  已知三角形三顶点为, 求的重心（即三角形三中线的公共点）的坐标。

解  设的三中线为, 其中顶点的对边上的中点为, 设重心为，

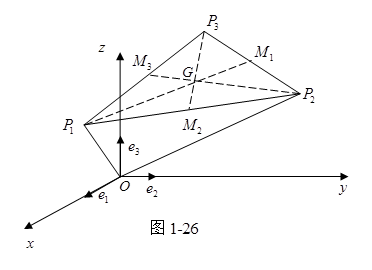
因为为的中点，即分成定比，所以根据公式（1.5-9）有

.

又因为    , 即重心把中线分成定比.

再根据公式（1.5-8）可得

,

 ，

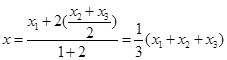所以之重心为

.