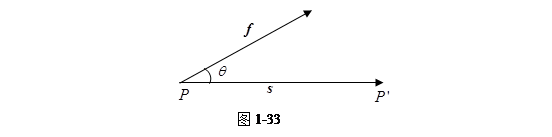
在物理学中，我们知道一个质点在力的作用下，经过位移那么这个力所作的功为   

,

其中为和的夹角（图1-33）。这里的功是由矢量和按上式确定的一个数量。类似的情况在其它问题中也常遇到(如求流体通过某一截面时的流速等等)。

定义1  两个矢量和的模与它们夹角的余弦的乘积称为矢量和的数量积 （也称内积或点积）, 记作或，即

.                   (1.7−1)

两个矢量的数量积是一个数量而不是矢量，特别的当两矢量中有一个为零矢量时， 例如, 那么, 从而有。

当为非零矢量时，有 射影

所以由（1.7-1）立刻得：

射影射影              (1.7−2)

特别地，当为单位矢量时，有

射影                      (1.7-2′)

如果（1.7-1）中的, 那么有我们把数量积称为的数量平方，并记作。

定理1   两矢量与相互垂直的充要条件是

证  当时，于是；

反过来， 当 时，如果均为非零矢量，那么根据（1.7-1）有

从而；如果中有零矢量，由于零矢量的方向任意，可以把它看成与任意矢量垂直，所以有。

下面我们讨论矢量的数性积的运算规律。

定理2   矢量的数量积满足下面的运算规律:

1）交换律

.             (1.7−3)

2）关于数因子的结合律

      (1.7−4)

3）分配律

        (1.7−5)

证    公式（1.7-3），（1.7-4），（1.7-5）中如果有零矢量，那么它们显然成立。

下面的证明，假设它们都是非零矢量。

1）.

2）如果, （1.7-4）显然成立；如果, 那么根据（1.7-2），（1.6-4）有

射影射影射影

而.

所以（1.7-4）成立。

3）根据（1.7-2），（1.6-3）有

射影射影射影射影射影

所以（1.7-5）式成立。

推论 1   .

根据矢量的数性积的这些运算规律可知，对于矢量数性积的运算，可以象多项式的乘法那样进行展开，例如

,

,

例1  证明平行四边形对角线的平方和等于它各边的平方和。

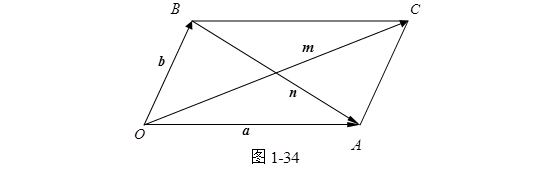
证  如图1-34，在平形四边形中，设两边为, 对角线, 那么

于是 ,

,

所以 ,

即 。       

例 2  试证如果一条直线与一个平面内的两条相交直线都有垂直，那么它就和平面内任何直线都垂直，即它垂直于平面。

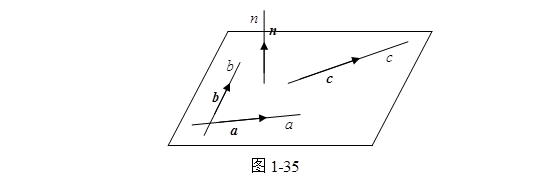
证  设直线与平面内两相交直线都垂直（图1-35）。下面证明与内与任意直线垂直。

在直线上分别任意取非零矢量，依条件有，所以

据已知，可用线性表示，即,

因而 .

这表明两矢量与互相垂直，也就是它们所在直线与互相垂直，从而直线垂直于平面。

例3  试证三角形的三条高交于一点.

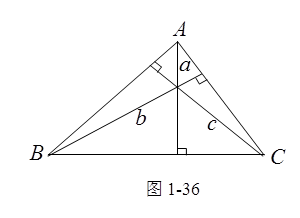
证  设的两边上的高交于点(图1-36),再设, ，那么

因为,所以,即;

又因为,所以,

即, 从而,即,

所以.

这就证明了点在第三条边的高线上，所以的三条高交于一点。

下面在直角坐标系下，用矢量的分量表示数性积。

定理3  设 ，, 则

.                (1.7−6)

证

 ,

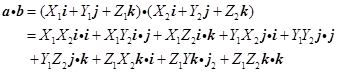因为是两两相互垂直的单位矢量,所以

且 ,

因而 .

推论2 设, 那么  

.               (1.7−7)

1）两点距离

因为在（1.7-1）中，当时有 ,

于是        ，或

定理4 设, 那么

.              (1.7−8)

证  根据（1.7-6）得

所以   ,

因而（1.7-8）式成立。

定理5  空间两点, 间的距离是

.         (1.7−9)

证  因为,

所以

2) 矢量的方向余弦

矢量与坐标轴（或坐标矢量）所成的角称为矢量的方向角,方向角的余弦称为矢量的方向余弦。一个矢量的方向完全可由它的方向角来决定。

矢量的方向余弦也可用矢量的分量来表示。

定理6  非零矢量的方向余弦是

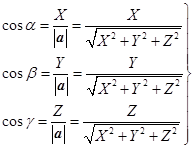               (1.7−10)

且

                 (1.7−11)

式中的分别为矢量与轴,轴,轴的交角，即矢量的三个方向角。

证   因为且,

所以             ,

从而             

同理可证（1.7-10）其余两式成立。由（1.7-10）立即可知（ 1.7-11）成立。

从定理6可以看出，空间的每一个矢量都可以由它的模与方向余弦决定，特别地 ，单位矢量的方向余弦等于它的分量，

即有                         (1.7−12)

3) 两矢量的交角

定理7   设空间中两个非零矢量为和,那么它们夹角的余弦是：

     （1.7-13）

证   因为

,

，

而

,

 ,

所以（1.7-13）成立。

推论4  矢量与相互垂直的充要条件是

                    (1.7-14)

在平面直角坐标系下，平面上的矢量也有完全类似的结论. 设平面上的两矢量为与, 那么有

                        (1.7− 6′)

                       (1.7− 7′)

                         (1.7− 8′)

平面上两点间的距离为

                (1.7− 9′)

矢量α的方向余弦可以表示为

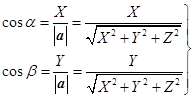                  (1.7−10′)

且

                        (1.7−11′)

4） 在平面上的情形，我们还可以单独用从到的有向角来决定矢量的方向。

   

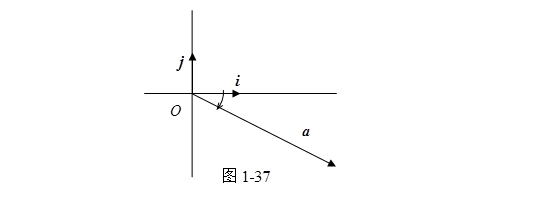
设, （图1-37），那么

,

 

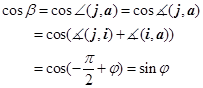
因此，平面上的非零矢量的方向，完全可由轴（或坐标矢量）到矢量的有向角  来决定，所以平面上的矢量可写成

               (1.7−12′)

矢量 a与 b的交角的余弦为

         (1.7−13′)

矢量 a与 b垂直的充要条件为

                  (1.7−1 4′)

例 4  已知三点, 且, 求：（1）与的夹角,(2) 在上的射影。

解 ：利用（1.5-1），（1.7-8）可得：

,

利用（1.7-6）可得：

,

,

因此可得  

（1）  

,

（2）  射影

 

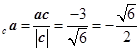
例 5  利用数性积证明柯西-施瓦兹(Cauchy-Schwarz)不等式

证                    ,

因为                    

而                   

所以                   ,

从而得                  ,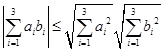

所以