当前位置:课程学习>>第一章>>学习内容>>文本学习>>知识点二
知识点二:矢量的加法
物理学中的力、位移、速度都是矢量。起点相同的两个不共线的力的合力、位移的合位移、速度的合速度,都可以用“平行四边形法则”求出。

如图1-3中的两个力![]() ,其合力就是以
,其合力就是以![]() 为邻边的平行四边形
为邻边的平行四边形![]() 的对角线矢量
的对角线矢量![]() 。两个力
。两个力![]() 与
与![]() 作用于
作用于![]() 的结果相当于力
的结果相当于力![]() 作用于
作用于![]() 的结果,可理解为矢量
的结果,可理解为矢量![]() 与矢量
与矢量![]() 相加的结果为矢量
相加的结果为矢量![]() 。
。
如图1-4中两个位移![]() ,其合位移就是以
,其合位移就是以![]() 为邻边的三角形的第三条边
为邻边的三角形的第三条边![]() 。连续两次位移
。连续两次位移![]() 与
与![]() 的结果相当于位移
的结果相当于位移![]() 的结果。可理解为矢量
的结果。可理解为矢量![]() 与矢量
与矢量![]() 相加的结果为矢量
相加的结果为矢量![]() 。
。
如图1-3,在自由矢量的意义下,两矢量![]() 合成的平行四边形法则可归结为三角形法则,只要平移矢量
合成的平行四边形法则可归结为三角形法则,只要平移矢量![]() 到
到![]() 的位置就可以了(即图1-4)。
的位置就可以了(即图1-4)。
由以上的讨论可抽象出自由矢量加法的定义。
定义1 设已知矢量![]() ,以空间中任意一点
,以空间中任意一点![]() 为始点,接连作矢量
为始点,接连作矢量![]() ,
,![]() 得一折线
得一折线![]() ,从折线的端点
,从折线的端点![]() 到另一端点
到另一端点![]() 的矢量
的矢量![]() 称为两矢量
称为两矢量![]() 与
与![]() 的和,记做
的和,记做![]() 。由两矢量
。由两矢量![]() 与
与![]() 求它们的和
求它们的和![]() 的运算称为矢量的加法。
的运算称为矢量的加法。
根据定义1与图1-4我们有
![]() (1.2.1)
(1.2.1)
这种求两个矢量和的法则称为三角形法则。由此可得:
定理1 如果以两个矢量![]() 为邻边组成一个平行四边形
为邻边组成一个平行四边形![]() ,那么对角线矢量
,那么对角线矢量![]() 。
。
这种求两个矢量和的法则称为平行四边形法则。特别的有![]()
定理2 矢量的加法满足下面的运算规律:
1) 交换律
![]() ; (1.2-2)
; (1.2-2)
2)结合律
![]() 。 (1.2-3)
。 (1.2-3)
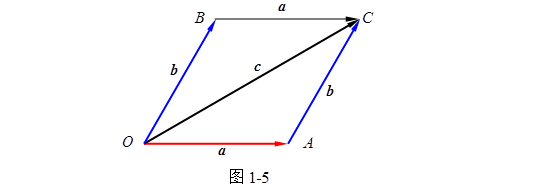
证
(1)对于两矢量![]() 不共线的情形,由图1-5可知
不共线的情形,由图1-5可知
![]() ,
,
![]()
所以
![]() 。
。
对于两矢量 a,b 共线的情形易证结论同样成立。
(2)
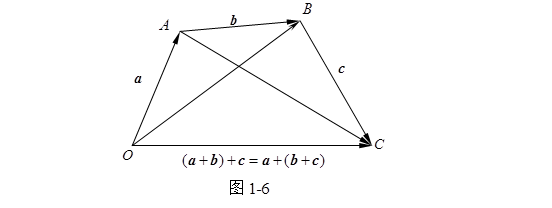
自空间任一点![]() 开始依次作
开始依次作![]() ,(图1-6),根据矢量加法定义有
,(图1-6),根据矢量加法定义有
![]()
![]()
所以
![]() .
.
由于矢量的加法满足交换律与结合律,所以三矢量 a,b,c 相加,不论它们的先后顺序与结合顺序如何,它们的和总是相同的, 因此可简单的写成 ![]() 。
。
推广到任意有限个矢量![]() 的和,就可以记做
的和,就可以记做![]()
有限个矢量![]() 相加的作图法,可以由矢量的 三角形求和法则推广如下: 自任意点
相加的作图法,可以由矢量的 三角形求和法则推广如下: 自任意点![]() 开始,依次引
开始,依次引 ![]() , 由此得一折线
, 由此得一折线![]() (图1-7),
(图1-7),

于是矢量![]() 就是 n 个矢量
就是 n 个矢量![]() 的和
的和
![]() .
.
即
![]() (1.2-4)
(1.2-4)
特别地当![]() 与
与![]() 重合时,它们的和为零矢量
重合时,它们的和为零矢量![]() 。
。
这种求和的方法称为多边形法则。
定义2 当矢量![]() 与矢量
与矢量![]() 的和等于矢量
的和等于矢量![]() ,即
,即![]() 时,我们称矢量
时,我们称矢量![]() 为矢量
为矢量![]() 与
与![]() 的差,并记做
的差,并记做![]() 。由两矢量
。由两矢量![]() 与
与![]() 求它们的差
求它们的差![]() 的运算称为矢量的减法。
的运算称为矢量的减法。
根据矢量加法的三角行法则,总有
![]() ,
,
所以由定义2得
![]() . (1.2-5)
. (1.2-5)
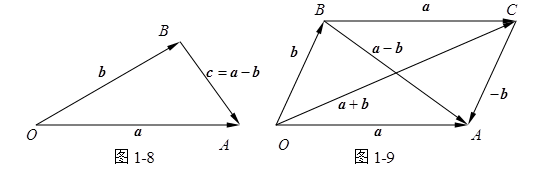
由此得到矢量减法的几何作图法:自空间任一点![]() 引矢量
引矢量 ![]() , 那么矢量
, 那么矢量![]() (图1-8)。如果以
(图1-8)。如果以![]() 为一对邻边构成平行四边形
为一对邻边构成平行四边形![]() ,那么显然它的一条对角线矢量
,那么显然它的一条对角线矢量![]() , 而另一条对角线矢量
, 而另一条对角线矢量![]() (图1-9)。
(图1-9)。
利用反矢量,可以把矢量的减法运算变为加法运算。
因为如果![]() ,即
,即![]() ,在等式两边各加
,在等式两边各加![]() 的反矢量
的反矢量![]() ,利用
,利用![]() ,便得
,便得![]() ,因此
,因此
![]() 。 (1.2-6)
。 (1.2-6)
这表明求![]() 与
与![]() 之差可以变为求
之差可以变为求![]() 与
与![]() 的反矢量
的反矢量![]() 之和。又因为
之和。又因为![]() 的反矢量就是
的反矢量就是![]() ,因此又可得
,因此又可得
![]() 。 (1.2-7)
。 (1.2-7)
从矢量减法的这个性质,可以得出矢量等式的移项法则:在矢量等式中, 将某一矢量从等号的一端移到另一端,只需改变它的符号。例如将等式![]() 中的
中的![]() 移到另一端,那么有
移到另一端,那么有![]() 。这是因为从等式
。这是因为从等式![]() 两边减去
两边减去![]() ,即加上
,即加上![]() ,而
,而![]() 的缘故。
的缘故。
我们还要指出,对于任何的两矢量![]() 与
与![]() ,有下列不等式
,有下列不等式
![]()
这个不等式还可以推广到任意有限多个矢量的情况:
![]() .
.
例 1 设互不共线的三矢量![]() 与
与![]() ,试证明顺次将它们的终点与始点相连而成一个三角形的充要条件是它们的和是零矢量。
,试证明顺次将它们的终点与始点相连而成一个三角形的充要条件是它们的和是零矢量。
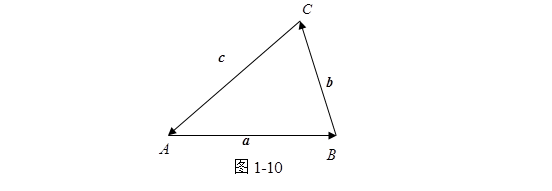
证 必要性 设三矢量![]() 可以构成三角形
可以构成三角形![]() ,即有
,即有
![]()
(图1-10),那么
![]() ,
,
即
![]() .
.
充分性 设![]() ,作
,作![]() , 那么
, 那么![]() , 所以
, 所以![]() , 从而
, 从而![]() 是
是![]() 的反矢量,因此
的反矢量,因此 ![]() , 所以
, 所以![]() 可构成一个三角形
可构成一个三角形![]() 。
。
例 2 如图1-11,在平行六面体![]() 中,
中,![]() , 试用
, 试用![]() 来表示对角线矢量
来表示对角线矢量![]() 。
。
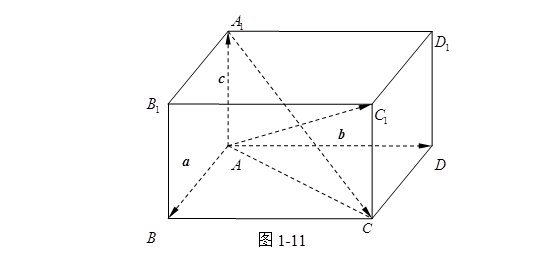
解
1) ![]()
2) ![]()
![]()
或者 ![]()
例 3 用矢量方法证明:对角线互相平分的四边形是平行四边形。
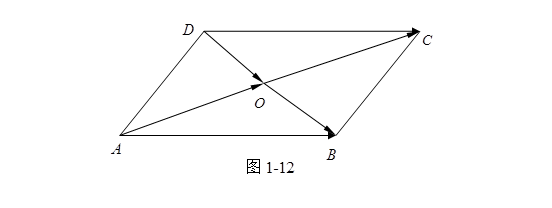
证 设四边形![]() 的对角线
的对角线![]() 交于
交于![]() 点且互相平分(图1-12),
点且互相平分(图1-12),![]()
从图可以看出:
![]()
因此,![]() ,且
,且![]() 即四边形
即四边形![]() 为平行四边形。
为平行四边形。
