当前位置:课程学习>>第一章>>学习内容>>文本学习>>知识点六
知识点六:矢量在轴上的射影
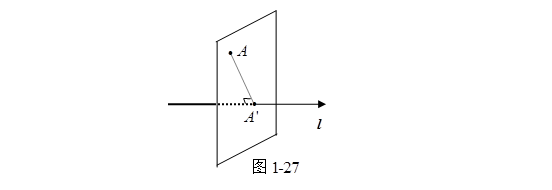
设已知空间的一点![]() 与一轴
与一轴![]() ,通过
,通过![]() 作垂直于轴
作垂直于轴![]() 的平面
的平面![]() ,我们把这个平面与轴
,我们把这个平面与轴![]() 的交点
的交点![]() 称为点
称为点![]() 在轴
在轴![]() 上的射影(图1-27)。
上的射影(图1-27)。
定义1 设矢量![]() 的始点
的始点![]() 和终点
和终点![]() 在轴
在轴![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么矢量
,那么矢量![]() 称为矢量
称为矢量![]() 在轴
在轴![]() 上的射影矢量(图1-28),记作射影矢量
上的射影矢量(图1-28),记作射影矢量![]() 。
。
如果在轴上取与轴同方向的单位矢量![]() ,那么有
,那么有
射影矢量![]()
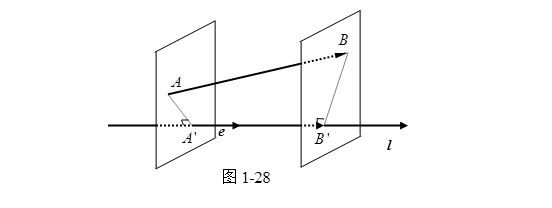
这里的![]() 称为矢量
称为矢量![]() 在轴
在轴![]() 上的射影,记做射影
上的射影,记做射影![]() ,
,
即射影![]()
![]() .
.
我们也可以把射影矢量![]() 与射影
与射影![]() 分别写为射影矢量
分别写为射影矢量![]() 与射影
与射影![]() ,
,
并且可以分别称为![]() 在
在![]() 上的射影矢量与
上的射影矢量与![]() 在
在![]() 上 的射影,两者之间的关系是:
上 的射影,两者之间的关系是:
射影矢量![]() =射影
=射影![]()
![]() (1.6-1)
(1.6-1)
射影![]() 的数值显然与
的数值显然与![]() 和
和![]() 的夹角的大小有关,现在来规定两矢量的夹角。
的夹角的大小有关,现在来规定两矢量的夹角。
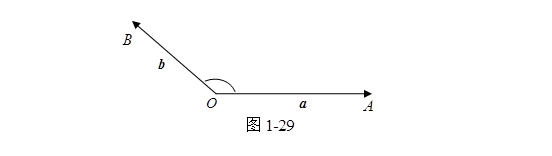
设![]() 是两个非零矢量,自空间任意点
是两个非零矢量,自空间任意点![]() 作
作![]() ,我们把由射线
,我们把由射线![]() 和
和![]() 构成的角度在
构成的角度在![]() 与
与![]() 之间的角(显然这角度与点
之间的角(显然这角度与点![]() 的选取无关)称为矢量
的选取无关)称为矢量![]() 与
与![]() 的夹角,记做
的夹角,记做![]() . 按规定,若
. 按规定,若![]() 与
与![]() 同向,那么
同向,那么![]() ;如果
;如果![]() 与
与![]() 反向,那么
反向,那么![]() ;如果
;如果![]() 不平行于
不平行于![]() ,那么
,那么![]() .
.
定理1 矢量![]() 在轴
在轴![]() 上的射影等于矢量的模乘以轴与该矢量的夹角的余弦:
上的射影等于矢量的模乘以轴与该矢量的夹角的余弦:
射影![]() (1.6-2)
(1.6-2)
证 当![]() 时,命题显然成立. 当
时,命题显然成立. 当![]() 时,过
时,过![]() 二点分别垂直于
二点分别垂直于![]() 轴的平面
轴的平面![]() , 它们与轴
, 它们与轴![]() 之交点分别是
之交点分别是![]() ,那么
,那么![]() 射影矢量
射影矢量![]() 。再作
。再作![]() , 易知终点
, 易知终点![]() 必在平面
必在平面![]() 上.
上.

因为![]() ,所以
,所以![]() ,
,![]() 为直角三角形,且
为直角三角形,且![]() (图1-30). 设
(图1-30). 设![]() 为轴
为轴![]() 上与
上与![]() 同方向的单位矢量,那么
同方向的单位矢量,那么
![]() 。
。
所以
![]() 射影
射影![]() 。
。
当![]() 时,
时,![]() 与
与![]() 同向,
同向,
![]()
当![]() 时, ,
时, ,![]() 与
与![]() 反向,
反向,
![]() ,
,
从而当![]() 时,总有
时,总有
射影![]() .
.
推论1 相等矢量在同一轴上的射影相等。
定理2 对于任何矢量![]() 有
有
射影![]() 射影
射影![]() 射影
射影![]() . (1.6-3)
. (1.6-3)
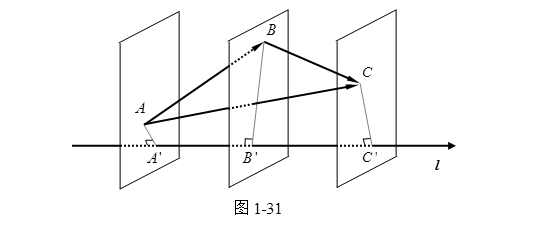
证 取![]() , 那么
, 那么![]() (图1-31) , 设
(图1-31) , 设![]() 分别 是
分别 是![]() 在轴
在轴![]() 上的射影,那么显然有
上的射影,那么显然有
;![]() ,
,
![]() 射影矢量
射影矢量![]() ,
,
![]() 射影矢量
射影矢量![]() ,
,
![]() 射影矢量
射影矢量![]()
射影矢量![]() 射影矢量
射影矢量![]() +射影矢量
+射影矢量![]() . 由(1.6-1)得
. 由(1.6-1)得
射影![]()
![]() =(射影
=(射影![]() 射影
射影![]()
其中![]() 为轴
为轴![]() 上与
上与![]() 同向的单位矢量,所以
同向的单位矢量,所以
射影![]() =射影
=射影![]() 射影
射影![]()
或
>射影![]() 射影
射影![]() 射影
射影![]()
定理3 对于任何矢量![]() 与任意实数
与任意实数![]() 有
有
射影![]() 射影
射影![]() . (1.6-4)
. (1.6-4)
证 如果![]() 或
或![]() , 命题显然成立.
, 命题显然成立.
设![]() ,
,![]() 且
且![]() , 那么当
, 那么当![]() 时,有
时,有
![]() ,
,
∴ 射影![]()
![]() 射影
射影![]()
当![]() 时,有
时,有
![]()
∴ 射影![]()
![]() 射影
射影![]()
因此(1.6-4)成立.
例 设在直角坐标系![]() 下,矢量
下,矢量![]() ,
,
试证明:射影![]() ,射影
,射影![]() ,射影
,射影![]() 。
。
证 设径矢![]() ,那么
,那么![]() 在坐标轴上的射影即为
在坐标轴上的射影即为![]() 在坐标轴上的射影.
在坐标轴上的射影.
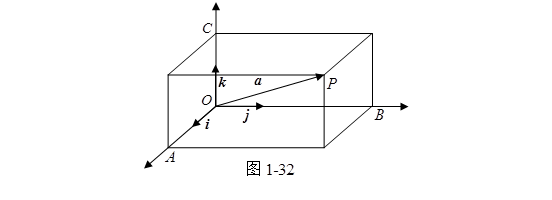
设![]() 点在
点在![]() 轴,
轴,![]() 轴,
轴,![]() 轴上的射影分别为
轴上的射影分别为![]() (图1-32),那么
(图1-32),那么
射影矢量![]() ,
,
射影矢量![]() ,
,
射影矢量![]() .
.
由矢量在轴上的射影定义得: 射影![]() ,射影
,射影![]() ,射影
,射影![]()
