定义1   两矢量与的外积（也称向量积或叉积）是一个矢量，记作,它的模是

                    （1.8-1） 

它的方向与和都垂直，并且按这个顺序构成右手标架（图1－38）

物理学中的力矩是一个矢量，这是两个矢量的外积的实例，如图1-39， 如果力的作用点是，，那么力矩

 

外积的性质

因为平行四边形的面积等于它两邻边长的积乘以夹角的正弦,所以由（1.8-1）得：

定理1  两个不共线矢量 与的外积的模，等于以与为边所构成的平行四边形的面积。

定理2  两矢量与共线的充要条件是

证：当与共线时（包括或为零矢量的情形），由（1.8-1）知，从而。反过来，当时，那么由（1.8-1）知， 或,或，或 ,因为零矢量可以看成与任何矢量共线，所以总有，命题得证。

定理3 矢量积是反交换的，即

                         （1.8-2）

证  如果与共线，那么与都是零矢量，这时定理显然成立。

如果与不共线，那么，即与的模相等；又根据矢量积的定义，与都同时垂直于与，因此与是两共线矢量，其次由于按顺序与分别构成右手标架与（图1-38），所以与的方向相反，从而得。

定理4 矢量积满足关于数因子的结合律，即

。                 （1.8-3）

式中为任意矢量，为任意实数。

证 若或共线，(1.8-3)显然成立。

若，且不共线，而

，

，

。

故三个矢量的模相等，其次容易知道这三个矢量当时，都和的方向相同，当时，都和的方向相反，因此三个矢量方向也相同，从而(1.8-3)成立。

推论1  设为任意实数，那么

。               (1.8-4)

定理5  矢量积满足分配律，即

               (1.8-5)

证  如果中至少有一个是零矢量或为一组共线矢量，(1.8-5)显然成立。现在假设不是上述情况，我们来证明(1.8-5)也成立。

设为的单位矢量，先证明下式成立：

                (1)

首先，我们可用下面的作图法作出矢量。

将矢量与置于公共始点，过点作平面垂直于（图1-40）。自矢量的终点引，为垂足，由此得矢量在上的射影矢量，再将在平面上绕点依顺时针方向（自的终点看向平面）旋转，得，那么。

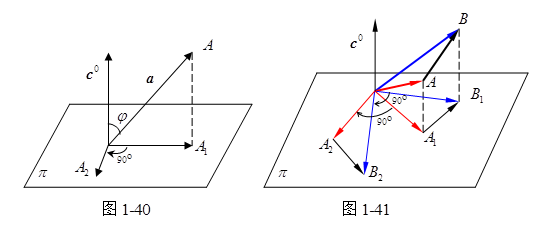
事实上，由作图法知，且构成右手标架，所以与同方向；如果设，那么，所以。

现在来证明（1）式，如图1-41所示，设，那么。并设分别为在垂直于的平面上的射影矢量，再将在平面内分别绕点依顺时针方向（自的终点看向平面）旋转得，依上述作图法可知，

而

所以

现在我们来证明（1.8-5）成立。

将(1)式两边乘以，利用(1.8-3)得 

而

所以

推论2                             (1.8-6)

证 

据矢量积满足这些运算规律，矢量积也可以象多项式的乘法那样进行展开，例如

。

但是必须注意矢量积不满足交换律，而具有反交换律，所以在矢量积的运算过程中，其因子矢量的次序不可以任意颠倒，如果交换矢量积的两个因子矢量，就必须改变符号，即换成它的反矢量。

例1  证明

证

例2  证明

               （1.8-7）

证  因为

，

所以

下面我们在右手直角坐标系上，用矢量的分量表示矢量积。

定理6  如果，那么

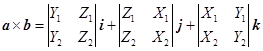       (1.8-8)

或写成      

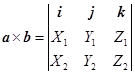                (1.8-9) 

证  因为

，

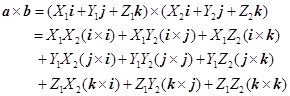又因为坐标矢量是三个两面互相垂直的单位矢量，所以有关系式

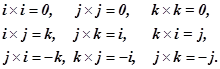          (1.8-10)

从面得

此即(1.8-8)式，利用三阶行列式可写成（1.8-9）。

例3  已知空是三点，试求（1）的面积；（2）的边上的高。

解  （1）的面积的面积，（如图1-42）

。

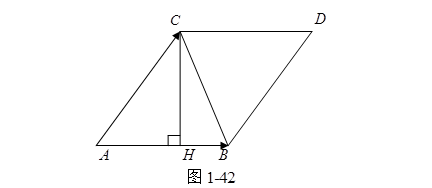
所以，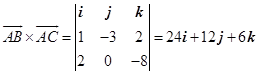

从而，

所以的面积。

（2）因为的边上的高即是的边上的高，所以

，

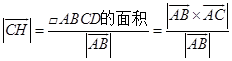又因为，

所以 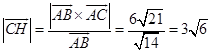。