学习指导

一、内容提要

1.基本概念

1）向量的定义；向量的加法运算；向量的数乘运算；两个向量的数量积；两个向量的向量积；三个向量的混合积；三个向量的双重向量积；

2）有限多个向量的线性相关、线性无关.

2.基本结论

1）两个向量共线的充要条件是它们线性相关；

2）三个向量共面的充要条件是它们线性相关；

3）空间中任意四个向量总是线性相关的；

4）两个向量垂直的充要条件是它们的数量积为零；

5）两个向量共线的充要条件是它们的向量积为零向量；

6）三个向量共面的充要条件是它们的混合积为零。

3.基本方法

1）在空间直角坐标系中计算两个向量的数量积的方法；

2）在空间直角坐标系中计算两个向量的向量积的坐标分量的方法；

3）在空间直角坐标系中计算三个向量的混合积的方法；

4）利用定比分点的定义求线段的分割点坐标分量的方法.

4.需要说明的问题

1）关于向量在仿射坐标系中的坐标分量问题.

可以利用向量加法运算的三角形法则，据已知条件运用待定系数法列出向量等式组，在利用取定坐标系下向量的坐标分量唯一，列出系数方程组求解。

2）关于两个向量的数量积问题.

两个向量的数量积既可以利用定义，也可以利用向量在轴上的射影的知识去计算，当然在空间直角坐标系下计算更为简便。

二、精选例题解析

例    已知三角形, 其中, 而分别是三角形两边上的点，且有, ,设与相交于图（1－19），试把矢量分解成的线性组合。

解  因为, 或

而     ,,

        

所以   ,    (1)

或            (2)

因此不共线，所以根据定理2，由(1),(2)得：

 

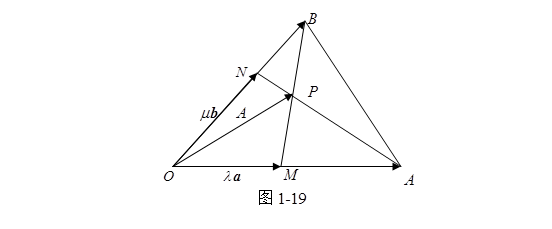
解得：

所以得： ,

即