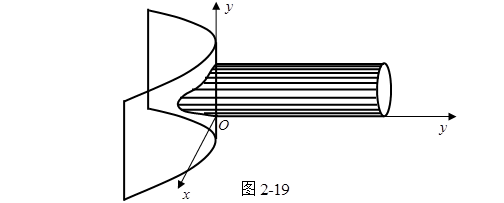当前位置:课程学习>>第二章>>学习内容>>视频课堂>>知识点四
知识点四:空间曲线的方程
空间曲线,可以看成两个曲面的交线。设
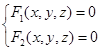 (2.4-1)
(2.4-1)
是这样的两个曲面方程,它们相交于曲线![]() 。这样曲线
。这样曲线![]() 上的任意点同时在两曲面上,它的坐标就满足方程组(2.4-1);反过来满足方程组(2.4-1)的任何一组解所决定的点,同时在两曲面上,即在两曲面的交线上,因此方程组(2.4-1)表示一条空间曲线的方程,我们把它叫做空间曲线的一般方程。
上的任意点同时在两曲面上,它的坐标就满足方程组(2.4-1);反过来满足方程组(2.4-1)的任何一组解所决定的点,同时在两曲面上,即在两曲面的交线上,因此方程组(2.4-1)表示一条空间曲线的方程,我们把它叫做空间曲线的一般方程。
从代数上知道,任何方程组的解,也一定是与它等价的方程的解,这说明空间曲线![]() 可能用不同形式的方程组来表达。
可能用不同形式的方程组来表达。
例1 写出![]() 轴的方程。
轴的方程。
解 ![]() 轴可以看成是两坐标平面
轴可以看成是两坐标平面![]() 与
与![]() 的交线,所以
的交线,所以![]() 轴的方程可以写成
轴的方程可以写成
![]() (1)
(1)
由于方程组(1)与方程组
![]() (2)
(2)
同解,所以![]() 轴的方程也可用(2)来表示。
轴的方程也可用(2)来表示。
例2 求在![]() 坐标面上,半径等于
坐标面上,半径等于![]() ,圆心为原点的圆的方程。
,圆心为原点的圆的方程。
解 因为空间的圆总可以看成是球面与平面的交线,在这里可以把所求的圆看成是以原点![]() 为球心,半径为
为球心,半径为![]() 的球面与
的球面与![]() 坐标平面的交线,所以所求的圆的方程为
坐标平面的交线,所以所求的圆的方程为
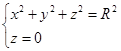 (3)
(3)
因为方程(3)与方程组
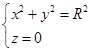 (4)
(4)
同解,所以所求圆的方程也可以用(4)来表达。这就是说所求圆也可以看成是以![]() 轴为对称轴,半径为
轴为对称轴,半径为![]() ,母线平行于
,母线平行于![]() 轴的圆柱面与
轴的圆柱面与![]() 坐标平面的交线。
坐标平面的交线。
因为球面![]() 与圆柱面
与圆柱面![]() 都通过所求的圆,所以所求圆的方程也可以用方程组
都通过所求的圆,所以所求圆的方程也可以用方程组
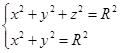
来表达。
空间曲线也象平面曲线那样,可用它的参数方程来表达,这是另一种表示空间曲线的常用方法,特别是把空间曲线看做质点的运动轨迹时,一般常采用参数表示法
空间曲线的参数方程与平面曲线的参数方程完全类同。在空间建立了坐标系后,设矢函数
![]() (2.4-2)
(2.4-2)
或
![]() (2.4-3)
(2.4-3)
当![]() 在区间
在区间![]() 内变动时,
内变动时,![]() 的终点
的终点![]() 全部都在空间曲线
全部都在空间曲线![]() 上;反过来,空间曲线
上;反过来,空间曲线![]() 上的任意点的径矢都可由
上的任意点的径矢都可由![]() 的某个值通过(2.4-2)或(2.4-3)来表示,那么(2.4-2)或(2.4-3)就叫做空间曲线
的某个值通过(2.4-2)或(2.4-3)来表示,那么(2.4-2)或(2.4-3)就叫做空间曲线![]() 的矢量式参数方程,其中
的矢量式参数方程,其中![]() 为参数。
为参数。
因为空间曲线上点的径矢![]() 的分量为
的分量为![]() ,所以空间曲线的参数方程常写成
,所以空间曲线的参数方程常写成
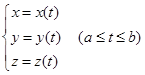 (2.4-4)
(2.4-4)
表达式(2.4-4)叫做空间曲线的坐标式参数方程,其中为参数。
例3 一个质点一方面绕一条轴线作等角速度的圆周运动,另一方面作平行于轴线的匀速直线运动,其速度与角速度成正比,求这个质点运动的轨迹方程。
解  在空间取标架
在空间取标架![]() ,使
,使![]() 轴重合于轴线,并设质点运动的起点为
轴重合于轴线,并设质点运动的起点为![]() ,质点作圆周运动的角速度为
,质点作圆周运动的角速度为![]() ,那么在
,那么在![]() 秒后质点从起点
秒后质点从起点![]() 运动到
运动到![]() 的位置(图2-17),
的位置(图2-17),![]() 在
在![]() 坐标面上的射影为
坐标面上的射影为![]() ,那么
,那么
![]()
(这里假设直线运动速度![]() 与角速度
与角速度![]() 之比为
之比为![]() ,即
,即![]() ),因此有
),因此有
![]()
![]() (2.4-5)
(2.4-5)
这就是质点运动轨迹的矢量式参数方程,其中![]() 为参数,它的坐标式参数方程为:
为参数,它的坐标式参数方程为:
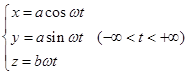 (2.4-6)
(2.4-6)
设![]() ,那么(2.4-5),(2.4-6)分别写成
,那么(2.4-5),(2.4-6)分别写成
![]() (2.4-5’)
(2.4-5’)
与
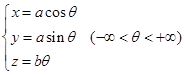 (2.4-6’)
(2.4-6’)
其中![]() 为参数,这条曲线叫做圆柱螺旋线。
为参数,这条曲线叫做圆柱螺旋线。
从(2.4-6’)消去参数![]() ,可以得到圆柱螺旋线方程的一般式为
,可以得到圆柱螺旋线方程的一般式为
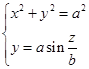 (2.4-7)
(2.4-7)
比较(2.4-6’)与(2.4-7),我们可以看出参数方程(2.4-6’)不仅表示出明确的质点运动的意义,而且从它也比较想象出轨迹的图形。因此在有些问题中,空间曲线的参数方程将显示出它的优越性。
例4 已知一半径为![]() 的球面与一个直径等于球的半径的圆柱面,如果圆柱面通过球心,那么这时球面与圆柱面的交线叫做维维安尼(Viviani)曲线,试建立维维安尼曲线的一般方程与参数方程。
的球面与一个直径等于球的半径的圆柱面,如果圆柱面通过球心,那么这时球面与圆柱面的交线叫做维维安尼(Viviani)曲线,试建立维维安尼曲线的一般方程与参数方程。
解 如图2-18所示,取球心为坐标原点,通过球心的圆柱面的一条母线为![]() 轴,过球心的圆柱面的直径为
轴,过球心的圆柱面的直径为![]() 轴建立右手直角坐标系,那么球面与圆柱面的方程分别为
轴建立右手直角坐标系,那么球面与圆柱面的方程分别为
![]() 与
与 ![]()
因此维维安尼曲线的一般方程为
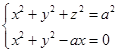 (5)
(5)
为了要求得维维安尼曲线的参数方程,我们也可以象把平面曲线的普通方程化为参数方程那样由(5)得到。先把(5)式中的圆柱面方程
![]()
利用平面上圆的参数方程改写为
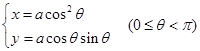
代入球面方程![]() 得
得
![]()
因此我们有
 (6)
(6)
与

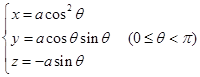 (7)
(7)
但如果令![]() ,即
,即![]() ,代入(7),那么(7)就变成(6)的形式
,代入(7),那么(7)就变成(6)的形式
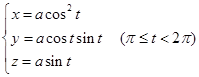
所以维维安尼曲线的参数方程为
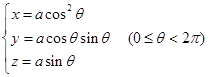
它的图形如图2-18所示。
通过空间曲线![]() 作柱面,使其母线平行于坐标轴
作柱面,使其母线平行于坐标轴![]() 或
或![]() 轴,设这样的柱面方程分别为
轴,设这样的柱面方程分别为
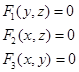 (2.4-8)
(2.4-8)
这三个柱面分别叫做曲线![]() 对
对![]() 与
与![]() 坐标面的射影柱面,因此(2.4-1)所表示的曲线
坐标面的射影柱面,因此(2.4-1)所表示的曲线![]() ,可以用它的对三个坐标面的任意两个射影柱面来表示。要求出(2.4-8),可以从(2.4-1)分别消去一个元而得到,因此在代数上从两个三元方程消去一个元,这样的几何意义就是求空间曲线
,可以用它的对三个坐标面的任意两个射影柱面来表示。要求出(2.4-8),可以从(2.4-1)分别消去一个元而得到,因此在代数上从两个三元方程消去一个元,这样的几何意义就是求空间曲线![]() 的射影柱面,例如从
的射影柱面,例如从
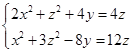
分别消去![]() 及
及![]() ,得
,得
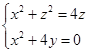
前一个射影柱面是一个准线在![]() 坐标面上的圆
坐标面上的圆
![]()
母线平行于![]() 轴的圆柱面,而后一个射影柱面是一个准线在
轴的圆柱面,而后一个射影柱面是一个准线在![]() 坐标面上的抛物线
坐标面上的抛物线![]() ,母线平行于
,母线平行于![]() 轴的抛物柱面,因此曲线可以看成是这两价目柱面的交线,它的形状如图2-19。从这里我们可以看到,得用空间曲线的射影柱面来表达维维安尼曲线,对我们认识空间曲线的形状是有限的。
轴的抛物柱面,因此曲线可以看成是这两价目柱面的交线,它的形状如图2-19。从这里我们可以看到,得用空间曲线的射影柱面来表达维维安尼曲线,对我们认识空间曲线的形状是有限的。