空间中平面与点的相关位置，有且只有两种情况，就是点在平面上，或点不在平面上，点在平面上的条件是点的坐标满足平面的方程。下面我们在直角坐标系下来讨论点不在平面上的情况。

1．点与平面间的距离

在求点与平面间的距离之前，我们先引进点关于平面的离差的概念。

定义1  如果自点引平面的垂线，其垂足为，那么矢量在平面的单位法矢量上的射影叫做点与平面间的离差，记做

射影                  (3.2-1)

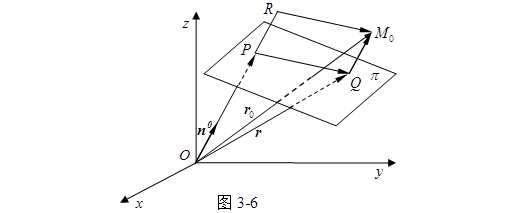
容易看出，空间的点与平面间的离差，当且仅当点位于平面的单位法矢量所指向的一侧（即与同向（图3-6））时，离差；在平面的另一侧（即与方向相反（图3-7））时，离差；当且仅当在平面上时，离差。

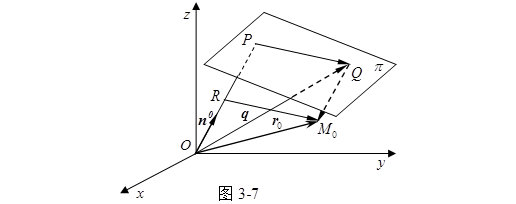
显然，离差的绝对值，就是点与平面之间的距离。

定理1  点与平面(3.1-13)间的离差为

                        (3.2-2)

这里。

证  根据定义3.2.1（图形3-6或图形3-7）得

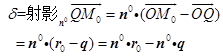
      而在平面(3.1-13)上，因此，所以

推论1  点与平面(3.1-14)间的离差是

           (3.2-3)

推论2  点与平面间的距离为

                (3.2-4)

2．平面划分空间问题、三元一次不等式的几何意义。

设平面的一般方程式为

那么，空间任何一点对平面的离差为

式中为平面的法化因子，所以有

                 (3.2-5)

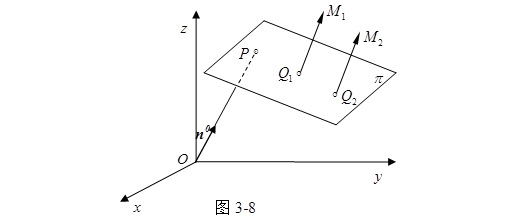
对于平面同侧的点，的符号相同，对于在异侧的点，有不同的符号。这是因为当与是同侧的点时，与同向；当与是异侧的点时与方向相反（图3-9）。因此由(3.2-5)式可以知道平面把空间划分为两部分，对于某一部分的点；而对于另一部分的点，则有，在平面上的点。