1．由直线上一点与直线的方向所决定的直线方程

在空间给定了一点与一个非零矢量，那么通过点且与矢量平行的直线就唯一地被确定，矢量叫做直线的方向矢量。显然任何一个与直线平行的非零矢量都可以作为直线的方向矢量。

在空间取标架，并设点的矢径为，直线上的任意点的矢径为（图3-11），那么显然点在直线上的充要条件为与共线，也就是

即             

所以

                          （3.4-1）

(3.4-1)叫做直线的矢量式参数方程，其中为参数。

如果设点，那么；又设，那么由(3.4-1)式得

                        (3.4-2)

(3.4-2)叫做直线的坐标式参数方程。

由(3.4-2)消去参数，那么得到

                  (3.4-3)

(3.4-3)叫做直线的对称式方程或直线的标准方程。

例1  求通过空间两点和的直线的方程。

解  取作为直线的方向矢量，设为直线上的任意点(图3-12)，那么

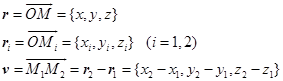
所以直线的矢量式参数方程为

                       (3.4-4)

坐标式参数方程为

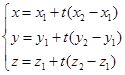                     (3.4-5)

对称式方程为

                   (3.4-6)

方程(3.4-4) , (3.4-5), (3.4-6)都叫做直线的两点式方程。

在直角坐标系下，直线的方向矢量常常取单位矢量

这时直线的参数方程为

                          (3.4-7)

或

                       (3.4-8)

直线的对称式方程为

                    (3.4-9)

这时(3.4-7)中的的绝对值恰好是直线上的两点与间的距离，这时因为

直线的方向矢量的方向角与方向余弦分叫做直线的方向角与方向余弦；直线的方向矢量的分量或与它成比例的一组数叫做直线的方向数。

由于与直线共线的任何非零矢量，都可以作为直线的方向矢量，因此 也可以分别看作是直线的方向角与方向余弦。

显然直线的方向余弦与方向数之间有着下面的关系：

      (3.4-10)

或

     (3.4-11)

由于这里所讨论的直线，一般都不是有向直线，而且两非零矢量与共线的充要条件为

或写成            

所以我们将用来表示与非零矢量共线的直线的方向（数）；同样在平面上用表示与矢量共线的直线的方向（数）。

2. 直线的一般方程

设有两个平面和的方程为

             （3.4-11）

如果，即方程组（3.4-11）中的系数行列式

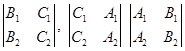
不全为零，那么平面和相交，它们的交线设为直线，因为直线的一任意一点同在两平面上，所以它的坐标必满足方程组（3.4-11）；反过来，坐标满足方程组（3.4-11）的点同在两平面上，因而一定在两平面的交线即直线上。因此方程组（3.4-11）表示直线的方程，我们把它叫做直线的一般式方程。

直线的标准方程（3.4-3）是一般方程的特殊情形。事实上，我们总可以将标准方程（3.4-3）表示为一般方程的形式，这是因为在（3.4-3）中不全为零，不妨设，那么（3.4-3）可先改写成

经过整理得下列形式：

                       （3.4-12）

式中

显然这是一各特殊的一般方程。（3.4-3）表示的直线可以看作是用（3.4-12）中两个方程表示的两个平面的交线，而这两个平面是通过该直线且分别平行于轴与轴的平面，在直角坐标系下它们又分别垂直于坐标面与（图3-13），我们把（3.4-12）叫做直线的射影式方程。

反过来，直线的一般方程（3.4-11）也总可以化为标准方程 (3.4-3）的形式，这是因为（3.4-11）中三个系数行列式

不全为零，不失一般性，设

那么由（3.4-11）中的两式分别消去与得直线的射影式方程为：

从而得直线的标准方程为

式中

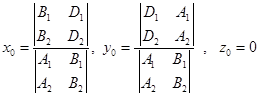
从上可以看出，给定了直线的一般方程(3.4-11)，我们立刻可以写出它的一组方向数，这就是方程组(3.4-11)的三个二阶系数行列式

由于这三个二阶行列式不能全为零，例如，那么我们就可使取任意指定的值（特别地可取），解方程组(3.4-11)得，那么为方程组(3.4-11)的一个特解，点就是直线上的一点，于是同样地得到了直线(3.4-11)的标准方程为

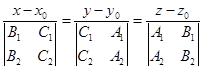
例2  化直线的一般方程

为标准方程。

解法一  因为的系数行列式

，

所以可由原方程组分别消去和，得直线的射影方程为：

所以直线的标准方程为

解法二  因为直线的方向数为

再设，解得，那么为直线上的一点，所以直线的标准方程为

 

在直角坐标系下，(3.4-11)中的两平面的法矢量分别为

所以直线的方向矢量可取为

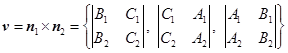
例3  把直线的一般方程

化为标准方程。

解  因为直线平行于矢量

所以矢量为直线的方向矢量。

其次由于

因此令，解方程组得，那么为直线上的一点，所以直线的标准方程为：