当前位置:课程学习>>第三章>>学习内容>>视频课堂>>知识点六
知识点六:空间两直线的相关位置
1.空间两直线的相关位置
空间两直线的相关位置有异面与共面两种情况,在共面中又有相交、平行与重合的三种情况。现在我们来导出这些相关位置成立的条件。
设两直线![]() 与
与![]() 的方程为:
的方程为:
![]() (1)
(1)
![]() (2)
(2)
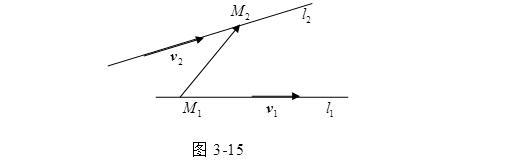
这里的直线![]() 是由点
是由点![]() 与矢量
与矢量![]() 决定的,
决定的,![]() 是由点
是由点![]() 与矢量
与矢量![]() 决定的。从图形3-15容易看出,两直线
决定的。从图形3-15容易看出,两直线![]() 与
与![]() 的相关位置决定于三矢量
的相关位置决定于三矢量![]() 的相互关系,当且仅当三矢量
的相互关系,当且仅当三矢量![]() 异面时,
异面时,![]() 与
与![]() 异面;当且仅当三矢量
异面;当且仅当三矢量![]() 共面时,
共面时,![]() 与
与![]() 共面;在共面的情况下,如果
共面;在共面的情况下,如果![]() 不平行于
不平行于![]() ,那么
,那么![]() 与
与![]() 相交,如果
相交,如果![]() 但不平行于
但不平行于![]() ,那么直线
,那么直线![]() 与
与![]() 平行,如果
平行,如果![]() ,那么
,那么![]() 与
与![]() 重合。因此我们就得到了下面的定理。记
重合。因此我们就得到了下面的定理。记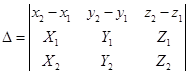
定理1 判断空间两直线(1)与(2)的相关位置的充要条件为
1)异面![]() (3.6-1)
(3.6-1)
2)相交![]() (3.6-2)
(3.6-2)
3)平行![]() (3.6-3)
(3.6-3)
4)重合![]() (3.6-4)
(3.6-4)
2.空间两直线的夹角
分别平行于空间两直线的两(非零)矢量的夹角,叫做空间两直线的夹角,如果用它们的方向矢量之间的夹角来表示,就是
![]()
或 ![]()
所以得:
定理2 在空间直角坐标系中,空间两直线(1)与(2)夹角的余弦为
![]() (3.6-5)
(3.6-5)
推论 两直线(1)与(2)垂直的充要条件是
![]() (3.6-6)
(3.6-6)
3.两异面直线间的距离与公垂线方程
空间两直线上的点之间的最短距离叫做这两条直线之间的距离。显然两相交或重合的直线间的距离等于零:两平行直线间的距离等于其中一直线上的任一点到另一直线的距离(点到直线的距离在下一节讨论);与两条异面直线都垂直相交的直线叫做两异面直线的公垂线,两异面直线间的距离显然就等于它们的公垂线夹于两异面直线间的线段的长。
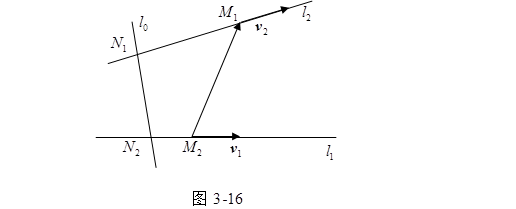
设两异面直线![]() 与它们的公垂线
与它们的公垂线![]() 的交点分别为
的交点分别为![]() ,那么
,那么![]() 与
与![]() 之间的距离。
之间的距离。
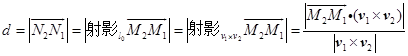
所以两异面直线(1)与(2)间的距离为
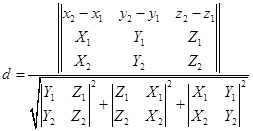 (3.6-7)
(3.6-7)
现在来求两异面直线(1),(2)的公垂线方程。如图3-16,公垂线![]() 的方向矢量可以取作
的方向矢量可以取作![]() ,而公垂线
,而公垂线![]() 可以看做由过
可以看做由过![]() 上的点
上的点![]() ,以
,以![]() 为方位矢量的平面与过
为方位矢量的平面与过![]() 上的点
上的点![]() ,以
,以![]() 为方位矢量的平面的交线,因此由(3.1-4)得公垂线的方程为:
为方位矢量的平面的交线,因此由(3.1-4)得公垂线的方程为:
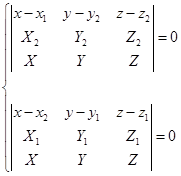 (3.6-8)
(3.6-8)
式中
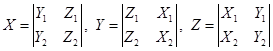
是矢量![]() 的分量,即
的分量,即![]() 的方向数。
的方向数。
例1 求通过点![]() 且与两直线
且与两直线
![]()
都相交的直线的方程。
解 设所求直线的方向矢量为![]() ,那么所求直线
,那么所求直线![]() 的方程可写成:
的方程可写成:
![]()
因为![]() 与
与![]() 都相交,而且
都相交,而且![]() 过点
过点![]() ,方向矢量为
,方向矢量为![]() ,
,![]() 过点
过点![]() ,方向矢量为
,方向矢量为![]() 。所以有
。所以有
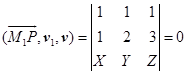 ,即
,即![]()
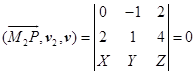 ,即
,即![]()
由上两式得: ![]()
显然又有
![]() ,即
,即![]()
![]() ,即
,即![]()
所以所求直线![]() 的方程为
的方程为
![]()
例2 已知两直线
![]()
试证明两直线![]() 与
与![]() 为异面直线,并求
为异面直线,并求![]() 与
与![]() 间的距离与它们的公垂线的方程。
间的距离与它们的公垂线的方程。
解 因为直线![]() 过点
过点![]() ,方向矢量为
,方向矢量为![]() ,而直线
,而直线![]() 过点
过点![]() ,方向矢量为
,方向矢量为![]() ,从而有
,从而有
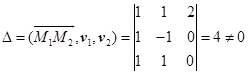
所以![]() 与
与![]() 为两异面直线。
为两异面直线。
又因为![]() 与
与![]() 的公垂线的方向矢量可取为
的公垂线的方向矢量可取为
![]()
所以![]() 与
与![]() 之间的距离为
之间的距离为
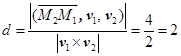
根据(3.6-8)得公垂线![]() 的方程为
的方程为
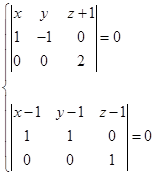
即
![]()
这条公垂线![]() 的方程又可写成
的方程又可写成
![]()
显然它就是![]() 轴。
轴。
