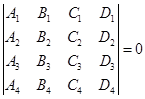定义1  空间中通过一条直线的所有平面的集合叫做有轴平面束，那条直线叫做平面束的轴。

定义2  空间中平行于同一个平面的所有平面的集合叫做平行平面束。

定理1  如果两个平面

                    （1）

                    （2）

交于一条直线，那么以直线为轴的有轴平面束的方程是：

           （3.8-1）

其中是不全为零的任意实数。

证  首先证明，当任取两不全为零的值时，（3.8-1）表示一个平面。把（3.8-1）改写为

        (3.8-1’)

这里的系数不能全为零，这是因为如果全为零，即

那么得

这和与是两相交平面的假设矛盾，因此(3.8-1’)是一个关于的一次方程，所以(3.8-1)或(3.8-1’)表示一个平面。

因为平面与的交线上的点的坐标同时满足方程（1）与（2），从而必满足方程(3.8-1)，所以(3.8-1)总代表通过直线的平面，也就是(3.8-1)总表示以直线为轴的平面束中的任意一个平面，

反过来，可以证明对于以直线为轴的平面束中的任意一个平面，我们都能确定使平面的方程为(3.8-1)的形式，为此只要在平面上选取不属于轴的任一点，那么由(3.8-1)表示的平面要通过点的条件是

所以

而不在轴上，所以，不能全为零，因此平面的方程可写为（3.8-1）的形式。

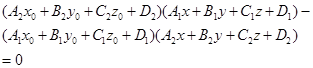，证毕。

定理2  如果两个平面

为平行平面，即，那么方程

表示平行平面束，平面束里任何一个平面都和平面或平行，其中是不全为零的任意实数，且

这个定理的证明类似于定理3.8.1，它的证明留给读者。

推论1  由平面决定的平行平面束（即与平面平行的全体平面）的方程是

                      (3.8-2)

其中是任意实数。

例1  求通过直线

且与平面垂直的平面方程。

解  设所求平面的方程为：

即       

由两平面垂直的条件它们的法向量相互垂直，故

即                  

因此                  

所求平面方程为

即               

例2  求与平面平行且在轴上截距等于-2的平面方程。

解  可设所求平面方程为：

因这平面在轴上截距为-2，所以这平面通过点（0，0，-2），由此得：

                    或者说  

因此所求方程为：      

例3  试证两直线

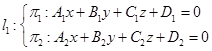
与

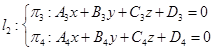
在同一平面上的充要条件是

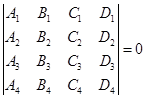                （3.8-3）

证  因为通过的任意平面为

其中是不全为零的任意实数；而通过的任意平面为

其中是不全为零的任意实数。因此两直线与在同一平面上的充要条件是存在不全为零的实数与使（3）与（4）代表同一平面，也就是（3）与（4）的左端仅相差一个不为零的数因子，即

化简整理得

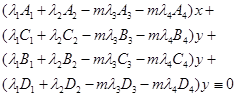
所以

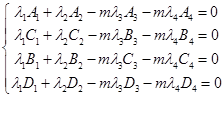
因为不全为零，所以得

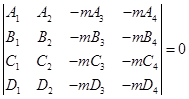
而，因此两直线与共面的充要条件为