空间两个平面的相关位置有三种情形，即相交、平行与重合，而且当仅当两平面有一部分公共点时它们相交，当且仅当两平面无公共点时它们相互平行，当且仅当一个平面上的所有点就是另一个平面的点时，这两平面重合。因此如果设两平面的方程为

                (1)

               (2)

那么两平面与是相交还是平行或是重合，取决于由方程（1）与（2）构成的方程组是有解还是无解，或是方程（1）与（2）仅相差一个不为零的因子，因此我们就得到了下面的定理。

定理1  两平面（1）与（2）

相交的充要条件为

               (3.3-1)

平行的充要条件为

                 (3.3-2)

重合的充要条件为

                 (3.3-3)

在直角坐标系下，由于两平面与的法矢量分别为

而当且仅当不平行于时，与相交；当且仅当时，与平行或重合。因此我们同样可得两平面与相交的充要条件为(3.3-1)，平行或重合的判定条件为

                     (3.3-4)

现在让我们在直角坐标系下来两平面的交角。

设两平面与间的二面角用来表示，而两平面的法矢量与的夹角记为，那么显然有（图3-10）。

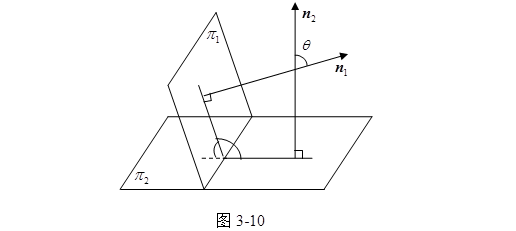
因此我们得到：

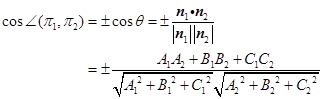        (3.3-5)

显然平面与互相垂直的充分必要条件为，即，因此从(3.3-5)我们得

定理2  两平面（1）与（2）相互垂直的充要条件为

                   (3.3-6)