当前位置:课程学习>>第三章>>拓展资源
学习指导
一、内容提要
1.基本概念
1)两条直线的夹角;直线与平面的夹角;两个平面的二面角;平面的法向量;直线方向角与方向余弦。
2)平行平面束;有轴平面束.
2.基本结论
1)平面![]() 与
与![]()
相交的充要条件为:
![]() ;
;
平行的充要条件为:
![]() ;
;
重合的充要条件为:
![]() 。
。
2)直线![]() 与平面
与平面![]()
相交的充要条件为:![]() ;
;
平行的充要条件为:![]() ;
;
直线在平面上的充要条件为![]() 。
。
3)直线![]() 与直线
与直线 ![]()
(记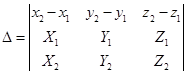 )
)
异面的充要条件为:![]() ;
;
相交的充要条件为:![]() ;
;
平行的充要条件为:![]() ;
;
重合的充要条件为:![]() 。
。
3.基本方法
1)在空间直角坐标系中运用两条直线的方向向量的数量积求两条直线的交角;
2)在空间直角坐标系中运用两条直线的方向向量的向量积求两条异面直线的公垂线的方向向量;
3)在空间直角坐标系运用两个平面的法向量的数量积求两个平面的二面角;
4.需要说明的问题
平面将空间进行划分的线性规划问题
利用点对平面的离差定义可以知道,平面将空间进行分割后,位于平面同侧的点的离差符号相同;异侧点的离差符号相反,即平面![]() 把空间划分为两部分,对于某一部分的点
把空间划分为两部分,对于某一部分的点![]() ;而对于另一部分的点,则有
;而对于另一部分的点,则有![]() 。
。
二、精选例题解析
例 已知两直线
![]()
试证明两直线![]() 与
与![]() 为异面直线,并求
为异面直线,并求![]() 与
与![]() 间的距离与它们的公垂线的方程。
间的距离与它们的公垂线的方程。
解 因为直线![]() 过点
过点![]() ,方向矢量为
,方向矢量为![]() ,而直线
,而直线![]() 过点
过点![]() ,方向矢量为
,方向矢量为![]() ,从而有
,从而有
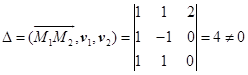
所以![]() 与
与![]() 为两异面直线。
为两异面直线。
又因为![]() 与
与![]() 的公垂线的方向矢量可取为
的公垂线的方向矢量可取为
![]()
所以![]() 与
与![]() 之间的距离为
之间的距离为
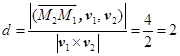
故公垂线![]() 的方程为
的方程为
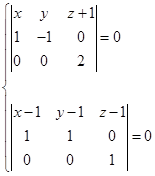
即
![]()
这条公垂线的方程又可写成
![]()
显然它就是![]() 轴。
轴。

