当前位置:课程学习>>第四章>>学习内容>>视频课堂>>知识点二
知识点二:锥面
定义 在空间,通过一定点且与定曲线相交的一族直线所生成的曲面叫做锥面,这些直线都叫做锥面的母线,那个定点叫做锥面的顶点,定曲线叫做锥面的准线。
设锥面的准线为
 (1)
(1)
顶点为![]() ,如果
,如果![]() 为准线上的任意点,那么锥面过点
为准线上的任意点,那么锥面过点![]() 的母线为:
的母线为:
![]() (2)
(2)
且有
![]() (3)
(3)
从(2),(3)四个等式消去参数![]() ,最后可得一个三元方程:
,最后可得一个三元方程:![]()
这就是以(1)为准线,![]() 为顶点的锥面方程。
为顶点的锥面方程。
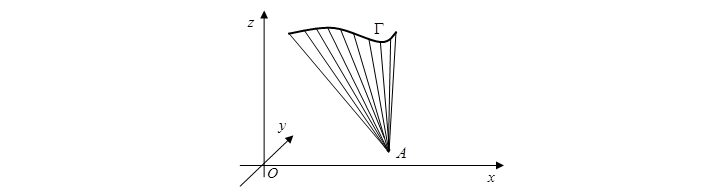
例1 锥面的顶点在原点,且准线为
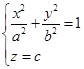
求锥面的方程。
解 设![]() 为准线上的任意点,那么过
为准线上的任意点,那么过![]() 的母线为:
的母线为:
![]() (4)
(4)
且有
![]() (5)
(5)
![]() (6)
(6)
由(4),(6)得
![]() (7)
(7)
(7)代入(5)得所求的锥面方程为:
![]()
这个锥面叫做二次锥面。
显然,锥面的准线不是唯一的,和一切母线都相交的每一条曲线,都可以做为它的准线。
例2 已知圆锥面的顶点为![]() ,轴垂直于平面
,轴垂直于平面![]() ,母线与轴成
,母线与轴成![]() 角。试求这个圆锥的方程。
角。试求这个圆锥的方程。
解 设![]() 为任一母线上的点,那么过
为任一母线上的点,那么过![]() 点的母线的方向矢量为
点的母线的方向矢量为
![]()
而在直角坐标系下,圆锥的轴线的方向即为平面![]() 的法方向,即为
的法方向,即为
![]()
根据题意有
![]()
即
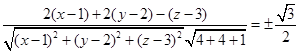
化简整理得所求的圆锥面的方程为
![]()
这是一个关于![]() 的齐次方程。
的齐次方程。
因为圆锥面是一种特殊的锥面,上面的解法是一种适合于圆锥面的特殊的方法,至于先求出圆锥面的准线,利用顶点与准线求锥面的一般方法,留给读者去完成。下面我们来证明一个关于锥面的定理。
定理 一个关于![]() 的齐次方程总表示顶点在坐标原点的锥面。
的齐次方程总表示顶点在坐标原点的锥面。
证 设关于![]() 的齐次方程为
的齐次方程为
![]() (8)
(8)
那么根据齐次方程的定义有
![]()
所以当![]() 时,有
时,有![]()
因此曲面过原点。
再设非原点![]() 满足(8),即有
满足(8),即有![]() ,那么直线
,那么直线![]() 的方程为
的方程为
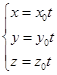
代入![]() 得
得 ![]()
所以整条直线都在曲面上,因此曲面(8)是由这种通过坐标原点的直线组成,即它是以原点为顶点的锥面。
在特殊情况下,关于![]() 的齐次方程可能只表示一个原点,这就是说除原点外,曲面上再也没有别的实点,例如
的齐次方程可能只表示一个原点,这就是说除原点外,曲面上再也没有别的实点,例如![]() 这样的曲面,我们又常常把它叫做具有实顶点的虚锥面。
这样的曲面,我们又常常把它叫做具有实顶点的虚锥面。
推论 关于![]() 的齐次方程表示顶点在
的齐次方程表示顶点在![]() 的锥面。
的锥面。
