当前位置:课程学习>>第四章>>学习内容>>视频课堂>>知识点三
知识点三:旋转曲面
定义 在空间,一条曲线![]() 绕着直线
绕着直线![]() 旋转一周所产生的曲面叫做旋转曲面,或称回转曲面。曲线
旋转一周所产生的曲面叫做旋转曲面,或称回转曲面。曲线![]() 叫做旋转曲面的母线,定直线
叫做旋转曲面的母线,定直线![]() 叫做旋转曲面的旋转轴,简称为轴。
叫做旋转曲面的旋转轴,简称为轴。
显然,旋转曲面的母线![]() 上的任意点
上的任意点![]() 在旋转时形成一个圆,这个圆也就是通过点
在旋转时形成一个圆,这个圆也就是通过点![]() 且垂直于轴
且垂直于轴![]() 的平面与旋转曲面的交线,我们把它叫做纬圆或称纬线。在通过旋转轴
的平面与旋转曲面的交线,我们把它叫做纬圆或称纬线。在通过旋转轴![]() 的平面上,以
的平面上,以![]() 为界的每个半平面都与曲面交成一条曲线,这些曲线显然在旋转中都能彼此重合,这曲线叫做旋转面的经线。
为界的每个半平面都与曲面交成一条曲线,这些曲线显然在旋转中都能彼此重合,这曲线叫做旋转面的经线。

现在来求旋转曲面的方程。
在空间直角坐标系下,设旋转曲面的母线为
 (1)
(1)
旋转轴为直线
![]() (2)
(2)
这里![]() 为轴
为轴![]() 上的一个定点,
上的一个定点,![]() 为旋转轴
为旋转轴![]() 的方向数。
的方向数。
设![]() 是母线
是母线![]() 上的任意点,那么过
上的任意点,那么过![]() 的纬圆总可以看成是过
的纬圆总可以看成是过![]() 且垂直于旋转轴
且垂直于旋转轴![]() 的平面与以
的平面与以![]() 为中心,
为中心,![]() 为半径的球面的交线,所以过
为半径的球面的交线,所以过![]() 的纬圆的方程为:
的纬圆的方程为:
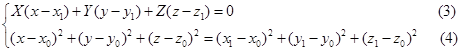
当点![]() 遍历整个母线
遍历整个母线![]() 时,就得出旋转曲面的所有的纬圆,这些纬圆生成旋转曲面。
时,就得出旋转曲面的所有的纬圆,这些纬圆生成旋转曲面。
又由于![]() 在母线
在母线![]() 上,所以又有
上,所以又有
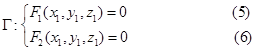
从(3),(4),(5),(6)四个等式消去参数![]() 最后得一个三元方程。
最后得一个三元方程。
![]()
这就是以(1)为母线,(2)为旋转轴的旋转曲面的方程。
例1 求直线![]() 绕直线
绕直线![]() 旋转所得的旋转曲面的方程。
旋转所得的旋转曲面的方程。
解 设![]() 是母线上的任意一点,因为旋转轴通过原点,所以过
是母线上的任意一点,因为旋转轴通过原点,所以过![]() 的纬圆方程是
的纬圆方程是
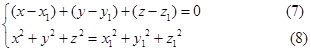
由于![]() 在母线上,所以又有
在母线上,所以又有
![]()
即
![]() (9)
(9)
由(7),(8),(9)三式消去![]() 得所求旋转曲面为
得所求旋转曲面为
![]()
即 ![]()
由于旋转曲面的经线,总可以作为最初的母线来产生旋转曲面。因此为了方便,今后总是取旋转曲面的某一条经线(显然是平面曲线)作为旋转曲面的母线。在直角坐标系下导出旋转曲面的方程时,我们又常把母线所在平面取作坐标面而旋转轴取做坐标轴,这时旋转曲面的方程具有特殊形式。
例2 母线所在坐标面![]() 面,旋转轴取做
面,旋转轴取做![]() 轴的旋转曲面方程。
轴的旋转曲面方程。
设旋转曲面的母线为
![]() (10)
(10)
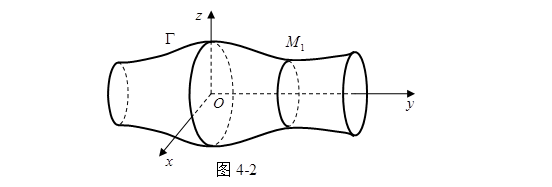
旋转轴为![]() 轴
轴
![]() (11)
(11)
如果![]() 为母线
为母线![]() 上的任意点,那么过
上的任意点,那么过![]() 的纬圆为
的纬圆为
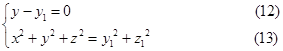
且有
![]() (14)
(14)
从(12),(13),(14)三式消去参数![]() 得所求旋转曲面的方程为
得所求旋转曲面的方程为
![]() (15)
(15)
同样,把曲线![]() 绕
绕![]() 轴旋转所得的旋转曲面的方程是
轴旋转所得的旋转曲面的方程是
![]() (16)
(16)
对于其他坐标面上的曲线,绕坐标轴旋转所得的旋转曲面,其方程可以类似的求出,这样我们就得出如下的规律:
当坐标平面上的曲线![]() 绕此坐标平面里的一个坐标轴旋转时,为了求出这样的旋转曲面的方程,只要将曲线
绕此坐标平面里的一个坐标轴旋转时,为了求出这样的旋转曲面的方程,只要将曲线![]() 在坐标面里的方程保留和旋转轴同名的坐标,而以其他两个坐标平方和的平方根来代替方程中的另一坐标。
在坐标面里的方程保留和旋转轴同名的坐标,而以其他两个坐标平方和的平方根来代替方程中的另一坐标。
例3 将椭圆
 (17)
(17)
分别绕长轴(即![]() 轴)与短轴(即
轴)与短轴(即![]() 轴)旋转,求所得旋转曲面的方程。
轴)旋转,求所得旋转曲面的方程。
解 因为旋转轴是![]() 轴,同名坐标就是
轴,同名坐标就是![]() ,在方程
,在方程![]() 中保留坐标
中保留坐标![]() 不变,用
不变,用![]() 代
代![]() ,便得椭圆(17)绕其长轴(即
,便得椭圆(17)绕其长轴(即![]() 轴)旋转曲面方程为
轴)旋转曲面方程为
![]() (4.3-1)
(4.3-1)
同样将椭圆(17)绕其短轴(即![]() 轴)旋转的曲面方程为
轴)旋转的曲面方程为
![]() (4.3-2)
(4.3-2)
曲面(4.3-1)叫做长形旋转椭球面(图4-3),曲面(4.3-2)叫做扁形旋转椭球面(图4-4)。

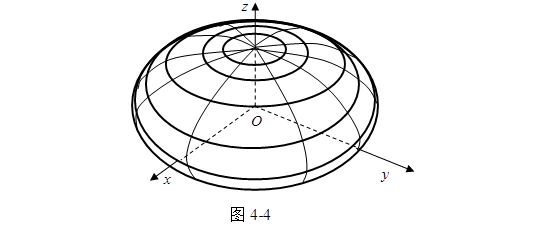
例4 将双曲线
 (18)
(18)
绕虚轴(即![]() 轴)旋转的旋转曲面方程为
轴)旋转的旋转曲面方程为
![]() (4.3-3)
(4.3-3)
绕实轴(即![]() 轴)旋转的旋转曲面方程为
轴)旋转的旋转曲面方程为
![]() (4.3-4)
(4.3-4)
曲面(4.3-3)叫做单叶旋转双曲面(图4-5),曲面(4.3-4)叫做双叶旋转双曲面(图4-6)。

例5 将抛物线
![]() (19)
(19)
绕它的对称轴旋转的旋转曲面方程为
![]() (4.3-5)
(4.3-5)
曲面(4.3-5)叫做旋转抛物面(图4-7)

例6 将圆
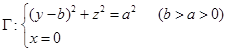 (20)
(20)
绕![]() 轴旋转所得旋转曲面的方程。
轴旋转所得旋转曲面的方程。
解 因为绕![]() 轴旋转,所以在方程
轴旋转,所以在方程![]() 中保留
中保留![]() 不变,而
不变,而![]() 用
用![]() 代,就得将圆(20)绕
代,就得将圆(20)绕![]() 轴旋转而成的旋转曲面方程为
轴旋转而成的旋转曲面方程为
![]()
即 ![]()
或 ![]()
这样的曲面叫做环面(图4-8),它的形状象救生圈。

