当前位置:课程学习>>第四章>>学习内容>>视频课堂>>知识点四
知识点四:椭球面
定义 在直角坐标系下,由方程
![]() (4.4-1)
(4.4-1)
所表示的曲面叫做椭球面,方程(4.4-1)叫做椭球面的标准方程,其中![]() 为任意的正常数,通常假定
为任意的正常数,通常假定![]() 。
。
现在我们从方程(4.4-1)出发来讨论椭球面的一些最简单的性质。
因为方程(4.4-1)仅含有坐标的平方项,可见当![]() 满足(4.4-1)时,点
满足(4.4-1)时,点![]() 也一定满足,其中正负号可任意选取,所以椭球面(4.4-1)关于三坐标平面,三坐标轴与坐标原点都对称。椭球面的对称平面,对称轴与对称中心分别叫做它的主平面,主轴与中心。椭球面(4.4-1)与它的三对称轴即坐标轴的交点分别为
也一定满足,其中正负号可任意选取,所以椭球面(4.4-1)关于三坐标平面,三坐标轴与坐标原点都对称。椭球面的对称平面,对称轴与对称中心分别叫做它的主平面,主轴与中心。椭球面(4.4-1)与它的三对称轴即坐标轴的交点分别为![]() ,这六个点叫做椭球面(4.4-1)的顶点。同一条对称轴上的两顶点间的线段以及它们的长度
,这六个点叫做椭球面(4.4-1)的顶点。同一条对称轴上的两顶点间的线段以及它们的长度![]() 与
与![]() 叫做椭球面(4.4-1)的轴,轴的一半即中心与各顶点间的线段及它们的长度
叫做椭球面(4.4-1)的轴,轴的一半即中心与各顶点间的线段及它们的长度![]() 与
与![]() 叫做椭球面(4.4-1)的半轴,当
叫做椭球面(4.4-1)的半轴,当![]() 时,
时,![]() 与
与![]() 分别叫做椭球面的长轴,中轴与短轴,而
分别叫做椭球面的长轴,中轴与短轴,而![]() 与
与![]() 分别叫做椭球面的长半轴,中半轴与短半轴。
分别叫做椭球面的长半轴,中半轴与短半轴。
显然任何两轴相等的椭球面一定是旋转椭球面。而三轴相等的椭球面就是球面。例如当![]() 时,方程(4.4-1)就变成(4.3-1),它是一个扁形旋转椭球面;而当
时,方程(4.4-1)就变成(4.3-1),它是一个扁形旋转椭球面;而当![]() 时,方程(4.4-1)就变成(4.3-2),而当
时,方程(4.4-1)就变成(4.3-2),而当![]() 时,方程(4.4-1)就变成(2.2-2),它是一个球面。所以旋转椭球面与球面都是椭球面(4.4-1)的特例。椭球面(4.4-1)当三轴不等时,叫做三轴椭球面。
时,方程(4.4-1)就变成(2.2-2),它是一个球面。所以旋转椭球面与球面都是椭球面(4.4-1)的特例。椭球面(4.4-1)当三轴不等时,叫做三轴椭球面。
因为椭球面(4.4-1)上的任何一点的坐标![]() 总有
总有
![]()
因此椭球面完全被封闭在一个长方体的内部,这个 长方体由六个平面:![]() 所组成。
所组成。
为了能够看出曲面的大致形状,我们考虑曲面与一组平行平面的交线,这些交线都是平面曲线,当我们对这些平面曲线的形状都已清楚时,曲面的大致形状也就看出来了,这就是所谓利用平行平面的截口来研究曲面图形的方法,简称为平行截割法,为了方便起见,常取与坐标面平行的一组平面。
如果用坐标面![]() 分别来截割球面(4.4-1),那么所得截口都是椭圆(图4-8),它们的方程分别是
分别来截割球面(4.4-1),那么所得截口都是椭圆(图4-8),它们的方程分别是
 (1)
(1)
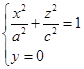 (2)
(2)
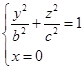 (3)
(3)
椭圆(1),(2),(3)叫做椭球面(4.4-1)的主截线(或主椭圆)。
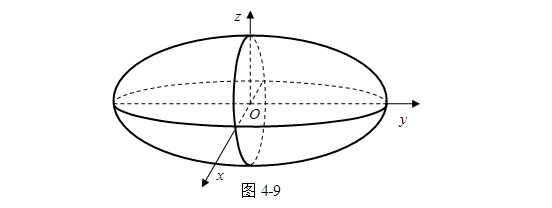
以下我们不妨取平行于![]() 坐标面的一组平行平面来截割椭球面(4.4-1),因为用平行于其它坐标面的平面来截割,情况类似。以平面
坐标面的一组平行平面来截割椭球面(4.4-1),因为用平行于其它坐标面的平面来截割,情况类似。以平面![]() 截割(4.4-1),得到的截线方程是
截割(4.4-1),得到的截线方程是
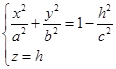 (4)
(4)
当![]() 时,(4)无图形,这表示平面
时,(4)无图形,这表示平面![]() 与椭球面(4.4-1)不相交;当
与椭球面(4.4-1)不相交;当![]() 时,(4)图形是平面
时,(4)图形是平面![]() 上的一个点
上的一个点![]() 或
或![]() ;当
;当![]() 时,(4)的图形是一个椭圆,这个椭圆的两半轴分别是
时,(4)的图形是一个椭圆,这个椭圆的两半轴分别是
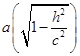 及
及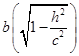
它的两轴的端点分别是![]() 与
与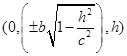 ,容易知道两轴的端点分别在椭圆(2)与(3)上(图4-9)。这样椭球面可以看成是由一个椭圆的变动(大小位置都改变)而产生的,这个椭圆在变动中保持所在平面与
,容易知道两轴的端点分别在椭圆(2)与(3)上(图4-9)。这样椭球面可以看成是由一个椭圆的变动(大小位置都改变)而产生的,这个椭圆在变动中保持所在平面与![]() 面平行,且两轴的端点分别在另外两个定椭圆(2)与(3)上滑动。
面平行,且两轴的端点分别在另外两个定椭圆(2)与(3)上滑动。
图4-9是椭球面(4.4-1)的图形。
椭球面的方程除了用标准方程(4.4-1)来表达外,也用参数方程
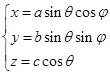 (4.4-2)
(4.4-2)
来表达,其中![]() 为参数。如果从 (4.4-2) 式中消去参数
为参数。如果从 (4.4-2) 式中消去参数![]() ,那么就得(4.4-1)。
,那么就得(4.4-1)。
例 已知椭球面的轴与坐标轴重合,且通过椭圆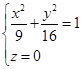 与点
与点![]() ,求这个椭球面的方程。
,求这个椭球面的方程。
解 所求椭球面的轴与三坐标轴重合,故设所求椭球面的方程为
![]()
它与![]() 面的交线为椭圆
面的交线为椭圆
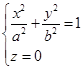
与已知椭圆
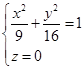
比较得
![]()
又因为椭球面通过点![]() ,所以又有
,所以又有
![]()
所以
![]()
因此所求椭球面的方程为
![]()
