定义  在空间，由平行于定方向且与一条定曲线相交的一族平行直线所产生的曲面叫做柱面，定方向叫做柱面的方向，定曲线叫做柱面的准线，那族平行直线中的每一条直线，都叫做柱面的母线。

设柱面的准线方程为

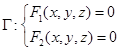                     (1)

母线的方向数为。如果为准线上的任意点，那么过点的母线方程为

                   (2)

且有

              (3)

（2）与(3）两组式子共有四个等式，从这四个等式消去参数，最后得一个三元方程 

这就是以（1）为准线，母线的方向数为的柱面方程。

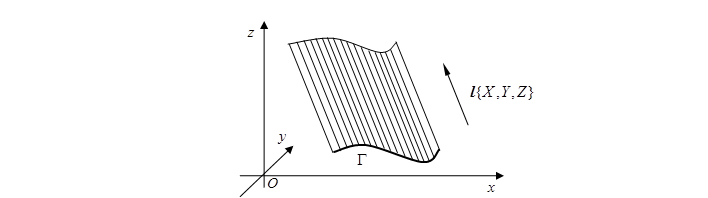
例1  柱面的准线方程为

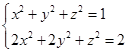
而母线的方向数是，求这柱面的方程。

解  设是准线上的点，那么过的母线为

且有                

                    (4)

                   (5)

再设             

      

那么               

               (6)

（6）代入（4）及（5）得：

                 (7)

               (8)

以2乘（7）再减去（8），得

所以              

                         (9)

（9）代入（7）或（8），即得所求的柱面的方程为 

即               

例2  已知圆柱面的轴为，点在此圆柱面上，求这个圆柱面的方程。

解法一  因为圆柱面的母线平行于其轴，所以母线的方向数即为轴的方向数1,-2,-2。如果能求出圆柱面的准线圆，那么再运用例1的解法，问题也就解决了。

空间的圆，总可以看成是某一球面与某一平面的交线，故这里的圆柱面的准线圆，可以看成是以轴上的点为中心，点到已知点()的距离为半径的球面与过已知点且垂直于轴的平面的交线，即准线圆的方程为

               (10)

再设为准线圆(10)上的点，那么有

且过的母线为

                   

由上四式消去参数即得所求的圆柱面的方程为

圆柱面是一种特殊的柱面，在特殊的情况下，除了一般解法外，往往还有其他特殊的解法。

如果将圆柱面看成是动点到轴线等距离点的轨迹，这里的距离就是圆柱面的半径，那么例2就有下面的第二种解法。

解法二  因为轴的方向矢量为，轴上的定点为，而圆柱面上的点为，所以，因此点到轴的距离为

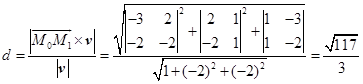
再设为圆柱面上的任意点，那么有

即

子           

化简整理得所求圆柱面的方程为