在平面上，由二元二次方程

       （1）

所表示的曲线，叫做二次曲线。在这一章里，我们将讨论二次曲线的几何性质，以及二次曲线方程的化简，最后对二次曲线进行分类。

我们在讨论中，将从研究直线与二次曲线的相交的问题入手，来认识二次曲线的某些几何性质。为了求直线与二次曲线的交点，就必须涉及到解二次方程的问题，但是二次方程的根可能是虚数，因此在这里我们将像代数中引进虚数把实数扩充成复数那样，在平面上引进虚元素。下面我们简单地说明一下有关虚元素的问题。

我们知道，当平面上建立了笛卡尔坐标系后，一对有序实数就表示平面上的一个点，如果及中至少有一个是虚数，那么在这里我们仍然认为表示平面上的一个点，这样的点我们把它叫做平面上的虚点，而叫做这一虚点的坐标，相应地我们把坐标是一对实数的点叫做平面上的实点。如果两个虚点对应的坐标都是共轭复数，那么这两点叫做一对共轭虚点，实点与虚点统称为复点。

当平面上引进了虚点之后，我们仍然可以讨论矢量、直线等概念，例如设与为平面上的两复点，那么我们称为以为起点，为终点的复矢量，并记做，如果与中至少有一为虚数时，我们把它叫做虚矢量；如果点的坐标满足表达式

，

其中为复数，我们就说点分成定比，特殊地把点叫做的中点；我们把

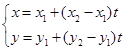
叫做由两点决定的直线的参数方程，式中为参数，它可为任意的复数。消去参数得：

式中。方程叫做直线的一般式方程，如果与三个实数成比例，那么直线为实直线，否则叫做虚直线。

必须指出，由于共轭复数之和为实数，所以连结两共轭虚点的线段的中点是实点。

平面上引进了虚点之后，曲线的方程中可能会出现虚系数，不过以后我们讨论问题时，只考虑实系数的曲线方程。但是由于引进了虚点，实系数方程所表示的曲线上将含有许多虚点，甚至有的实系数方程所表示的曲线上只有虚点而无实点。

为了方便起见，我们引进下面的一些记号：

这样我们容易验证，下面的恒等式成立：

          （2）

（1）式也就可以写成

于       （3）

我们把的系数所排成的矩阵

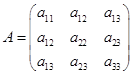
叫做二次曲线（1）的矩阵（或称的矩阵），而用的系数所排成的矩阵

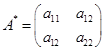
叫做的矩阵。显然二次曲线（1）的矩阵的第一，第二与第三行的元素分别是的系数。

今后我们还常常要引用下面的几个符号：

，，，

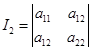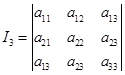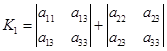
这里的是矩阵的主对角元素的和，是矩阵的行列式，是矩阵的行列式，而的两项是的两项分别添加上两条“边”而成的两个二阶行列式，这添加上的两条“边”的元素是矩阵中的第三行与第三列的对应元素，也就是说用二阶行列式

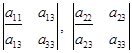
分别代替中的就由得到。