当前位置:课程学习>>第五章>>学习内容>>视频课堂>>知识点三
知识点三:二次曲线的渐近方向、中心、渐近线
1.二次曲线的渐近方向
上一节中,我们知道,二次曲线
![]() (1)
(1)
和具有方向![]() 的直线
的直线
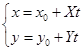 (2)
(2)
当满足条件
![]() (3)
(3)
时,或者只有一个实交点,或者没有交点,或者直线(2)全部在二次曲线(1)上,成为二次曲线的组成部分。
定义1 满足条件![]() 的方向
的方向![]() 叫做二次曲线(1)的渐近方向,否则叫做非渐近方向。
叫做二次曲线(1)的渐近方向,否则叫做非渐近方向。
因为二次曲线(1)的二次项系数不能全为零,所以渐近方向![]() 所满足的(3)总有确定的解。
所满足的(3)总有确定的解。
如果![]() ,那么把(3)改写成
,那么把(3)改写成
![]()
得
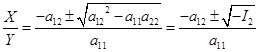
如果![]() ,把(3)改写成
,把(3)改写成
![]()
得
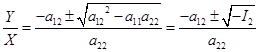
如果![]() ,那么一定有
,那么一定有![]() ,这时(3)变为
,这时(3)变为
![]()
即 ![]() 或
或 ![]()
这时 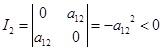
从上我们看到,当且仅当![]() 时,二次曲线(1)的渐近方向是一对共轭的虚方向;
时,二次曲线(1)的渐近方向是一对共轭的虚方向;![]() 时,(1)有一个实渐近方向;
时,(1)有一个实渐近方向;![]() 时,(1)有两个不同的实渐近方向。因此二次曲线的渐近方向最多有两个,显然二次曲线的非渐近方向有无数多。
时,(1)有两个不同的实渐近方向。因此二次曲线的渐近方向最多有两个,显然二次曲线的非渐近方向有无数多。
定义2 没有实渐近方向的二次曲线叫做椭圆型的,有一个实渐近方向的二次曲线叫做抛物型的,有两个不同的实渐近方向的二次曲线叫做双曲型的。
因此二次曲线(1)按其渐近方向可能分为三种类型,即
(1)椭圆型曲线:![]()
(2)抛物型曲线:![]()
(3)双曲型曲线:![]()
2.二次曲线的中心与渐近线
上一节中,我们知道,当直线(2)的方向![]() 为二次曲线(1)的非渐近方向时,
为二次曲线(1)的非渐近方向时,
即当 ![]() 时,
时,
直线(2)与二次曲线(1)总交于两个点(两不同的实点,两重合的实点或一对共轭虚点)。我们把由这两点决定的线段叫做二次曲线的弦。
定义3 如果点![]() 是二次曲线的通过它的所有弦的中点(因而
是二次曲线的通过它的所有弦的中点(因而![]() 是二次曲线的对称中心),那么点
是二次曲线的对称中心),那么点![]() 叫做二次曲线的中心。
叫做二次曲线的中心。
根据这个定义,当点![]() 为二次曲线(1)的中心时,那么过
为二次曲线(1)的中心时,那么过![]() 以(1)的任意非渐近方向
以(1)的任意非渐近方向![]() 为方向的直线(2)与二次曲线(1)交于两点
为方向的直线(2)与二次曲线(1)交于两点![]() ,点
,点![]() 就是弦
就是弦![]() 的中点。因此将(2)代入(1)得
的中点。因此将(2)代入(1)得
![]()
此时有 ![]()
即
![]()
因为![]() 为任意非渐近方向,所以(4)式是关于
为任意非渐近方向,所以(4)式是关于![]() 的恒等式,从而有
的恒等式,从而有
![]()
反过来,适合上面两式的点![]() ,显然是二次曲线的中心。
,显然是二次曲线的中心。
这样我们就得到了下面的定理:
定理1: 点![]() 是二次曲线(1)的中心,其充要条件是
是二次曲线(1)的中心,其充要条件是
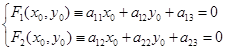 (5.2-1)
(5.2-1)
推论 坐标原点是二次曲线的中心,其充要条件是曲线方程里不含![]() 与
与![]() 的一次项。
的一次项。
所以,二次曲线(1)的中心坐标由下列方程组决定
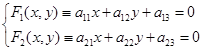 (5.2-2)
(5.2-2)
如果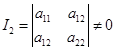 ,那么(5.2-2)有唯一解,这时二次曲线(1)将有唯一中心,(5.2-2)的解即为中心的坐标。
,那么(5.2-2)有唯一解,这时二次曲线(1)将有唯一中心,(5.2-2)的解即为中心的坐标。
如果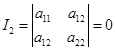 ,即
,即![]() ,那么当
,那么当![]() 时,(5.2-2)无解,二次曲线(1)没有中心;而当
时,(5.2-2)无解,二次曲线(1)没有中心;而当![]() 时,(5.2-2)有无数多解,这时直线
时,(5.2-2)有无数多解,这时直线![]() (或
(或![]() )上的所有点都是二次曲线(1)的中心,这条直线叫做中心直线。
)上的所有点都是二次曲线(1)的中心,这条直线叫做中心直线。
定义4 有唯一中心的二次曲线叫做中心二次曲线,没有中心的二次曲线叫做无心二次曲线,有一条中心直线的二次曲线叫做线心二次曲线,无心二次曲线与线心二次曲线统称为非中心二次曲线。
根据这个定义与(5.2-2),我们得二次曲线(1)按其中心的分类:
(1)中心曲线: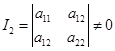 ;
;
(2)非中心曲线;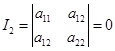 ,即
,即![]() ,
,
1) 无心曲线:![]() ,
,
2)线心曲线:![]() 。
。
从二次曲线的按渐近方向与按中心的两种初步的分类中,容易看出,椭圆型曲线与双曲型曲线都是中心曲线,而抛物型曲线是非中心曲线,它包括无心曲线与线心曲线。
定义5 通过二次曲线的中心,而且以渐近方向为方向的直线叫做这二次曲线的渐近线。
显然,椭圆型曲线只有两条虚渐近线而无实渐近线,双曲型曲线有两条实渐近线,而抛物型曲线中的无心曲线无渐近线,至于线心曲线它有一条实渐近线,就是它的中心直线。
定理2 二次曲线的渐近线与这二次曲线或者没有交点,或者整条直线在这二次曲线上,成为二次曲线的组成部分。
证 设直线(2)是二次曲线(1)的渐近线,这里![]() 为二次曲线的中心,
为二次曲线的中心,![]() 为二次曲线的渐近方向,那么我们有
为二次曲线的渐近方向,那么我们有
![]()
因此根据上一节中的直线与二次曲线的相交情况的讨论,我们有:当点![]() 不在二次曲线(1)上,即
不在二次曲线(1)上,即![]() 时,渐近线(2)与二次曲线(1)没有交点;当点
时,渐近线(2)与二次曲线(1)没有交点;当点![]() 在二次曲线(1)上,即
在二次曲线(1)上,即![]() 时,渐近线(2)全部在二次曲线上,成为二次曲线的组成部分。
时,渐近线(2)全部在二次曲线上,成为二次曲线的组成部分。
